인프런의 영리한 프로그래밍을 위한 알고리즘 강좌를 보고 작성한 문서입니다.

그래프

(무방향) 그래프 G = (V, E)

• V : 노드(node) 혹은 정점(vertex)

• E : 노드쌍을 연결하는 에지(edge) 혹은 링크(link)

• 개체(object)들 간의 이진관계를 표현

• n=|V|, m=|E|

  

방향 그래프와 가중치 그래프

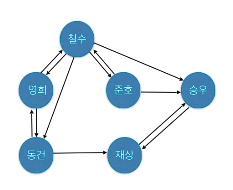
방향그래프(Directed Graph) G = (V, E)

• 에지 (u, v)는 u로부터 v로의 방향을 가짐

가중치(weighted) 그래프

• 에지마다 가중치(weight)가 지정

그래프의 표현

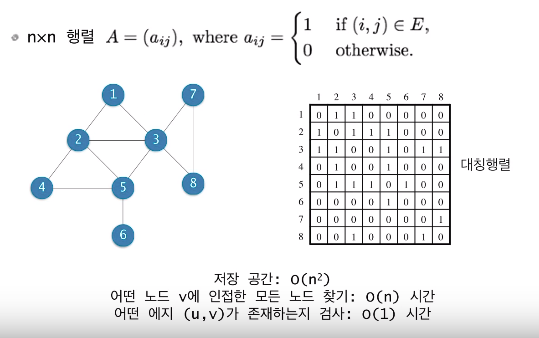
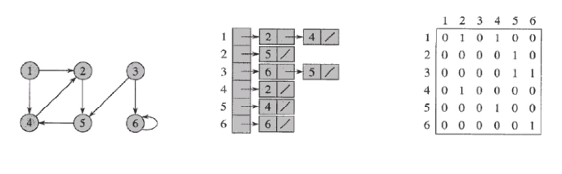
인접행렬 (adjacency matrix)

인접리스트 (adjacency list)

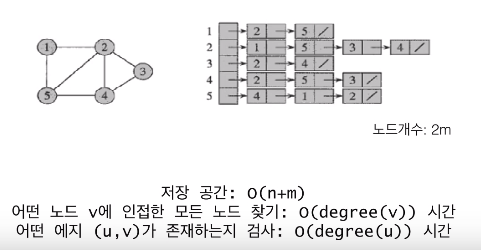
• 정점 집합을 표현하는 하나의 배열과
• 각 정점마다 인접한 정점들의 연결 리스트

방향 그래프

• 인접행렬은 비대칭

• 인접 리스트는 m개의 노드를 가짐

  

가중치 그래프의 인접행렬 표현

에지의 존재를 나타내는 값으로 1대신 에지의 가중치를 저장

에지가 없을 때 혹은 대각선:

• 특별히 정해진 규칙은 없으며, 그래프와 가중치가 의미하는 바에 따라서

• 예: 가중치가 거리 혹은 비용을 의미하는 경우라면 에지가 없으면 ∞, 대각선은 0

• 예: 만약 가중치가 용량을 의미한다면 에지가 없을때 0, 대각선은 ∞
  (대각선은 자기자신을 의미)

경로와 연결성

• 무방향 그래프 G = (V, E)에서 노드 u와 v를 연결하는 경로(path)가 존재할 때 v와 u는 서로 연결되어 있다고 말함

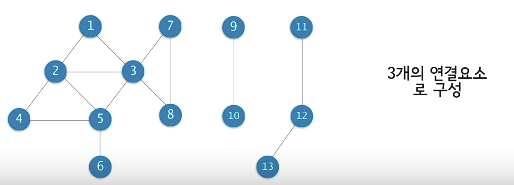
• 모든 노드 쌍들이 서로 연결된 그래프를 연결된(connected) 그래프라고 한다.

• 연결요소 (connected component)