인프런의 영리한 프로그래밍을 위한 알고리즘 강좌를 보고 작성한 문서입니다.

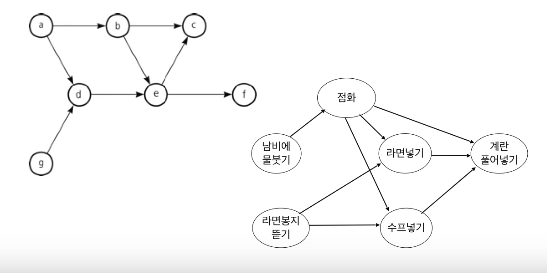
서로소인 집합들의 표현

• 각 집합을 하나의 트리로 표현

• 예 : 2개의 집합

  

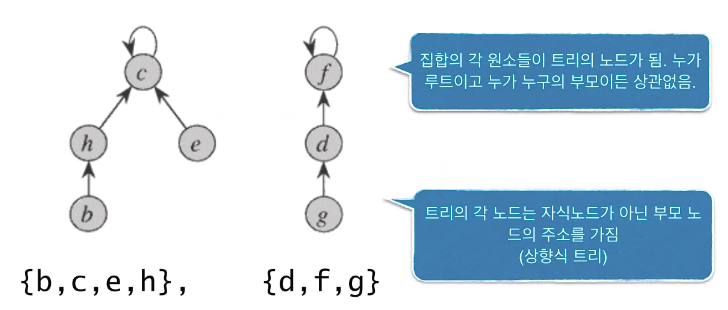
• 누가 부모인지는 중요하지 않다.

  

  

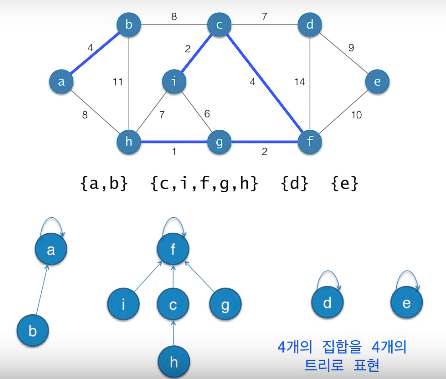
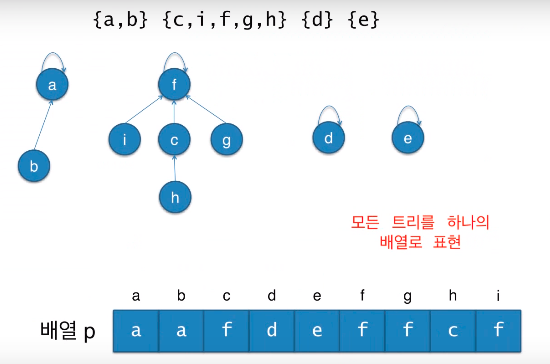
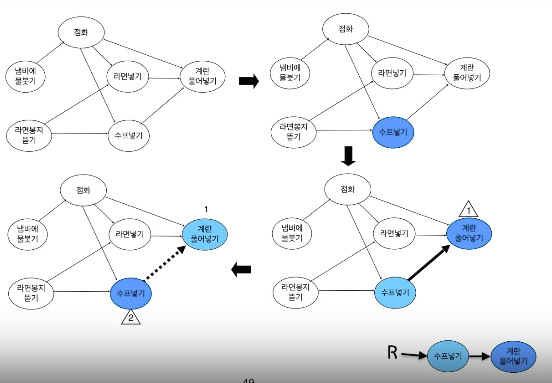
Find-Set(v)

• 자신이 속한 트리의 루트를 찾음

  

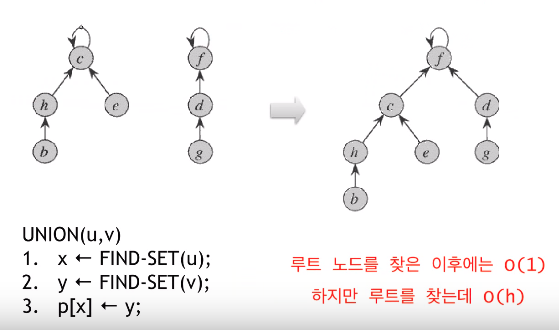
Union(u, v)

• 한 트리의 루트를 다른 트리의 루트의 자식 노드로 만듬

  

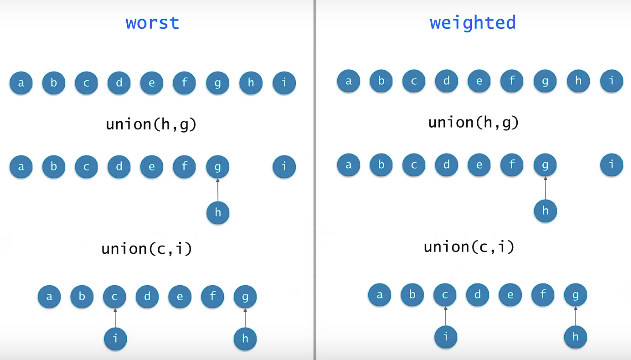
Weighted Union

• 두 집합을 union할 때 작은 트리의 루트를 큰 트리의 루트의 자식으로 만듬 (여기서 크기란 노드의 개수)

• 각 트리의 크기(노드의 개수)를 카운트하고 있어야

  

Worst vs Weighted Union

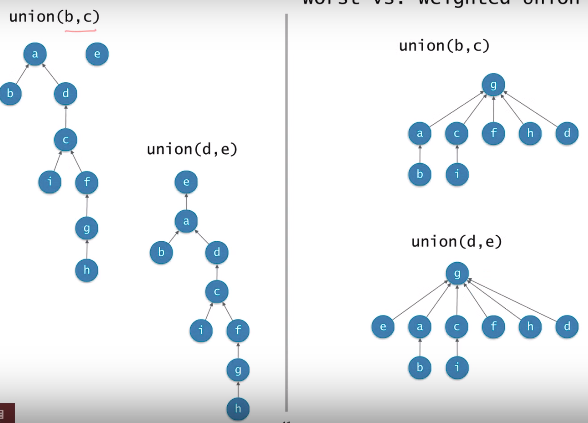
Path Compression

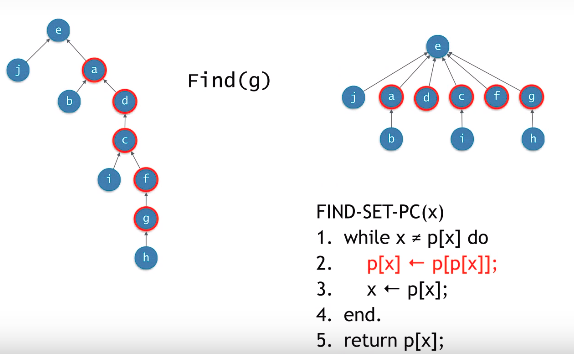
• 다 루트의 자식들로 만들어 간다.

• find를 하면서 찾기만 하지 않고 루트의 자식으로 만들어 버려서 높이를 낮춘다.

• 간단하게는 처음 루트를 찾고 다시 한번 반복하여 루트에다가 옮긴다.

• FIND-SET-PC(x)에 빨간 코드를 이용하면 루트에 옮기는게 아니라 자신의 부모의 부모에다 옮기는 형식으로 한다.(Find한 경로를 절반의 높이로 만든다.)

Weighted Union with Path Compression (WUPC)

log*(로그 스타) 함수란?

• (log log log … log N) 이렇게 로그를 여러번 했을때 1이 되는 횟수

• 5보다 클 일이 없는 수(현실에서는 거의 불가능)

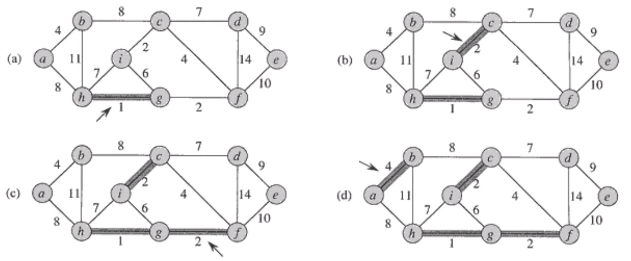
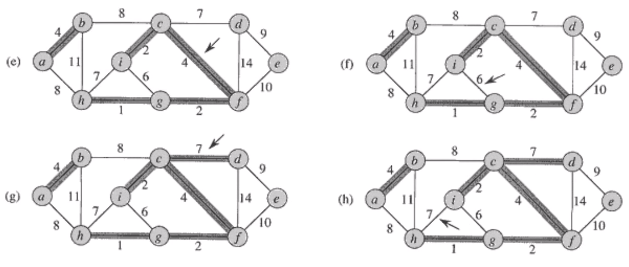
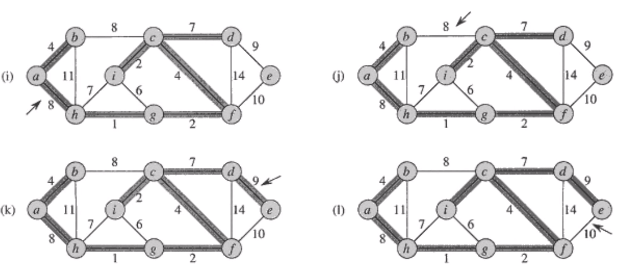
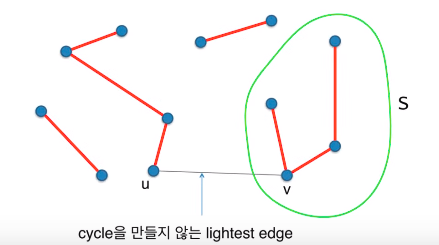
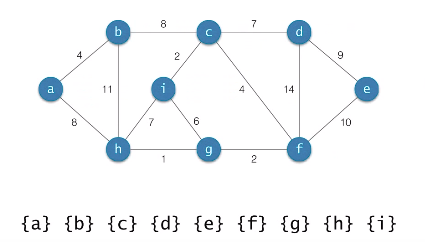
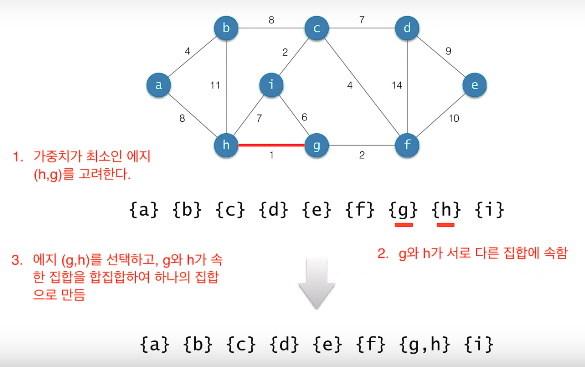
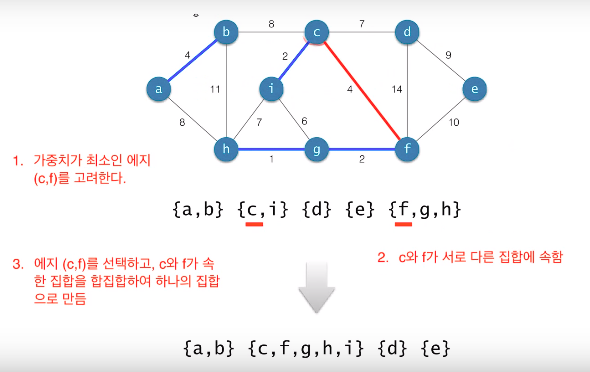
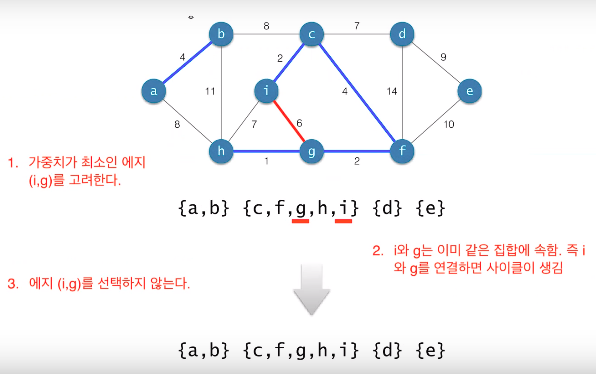
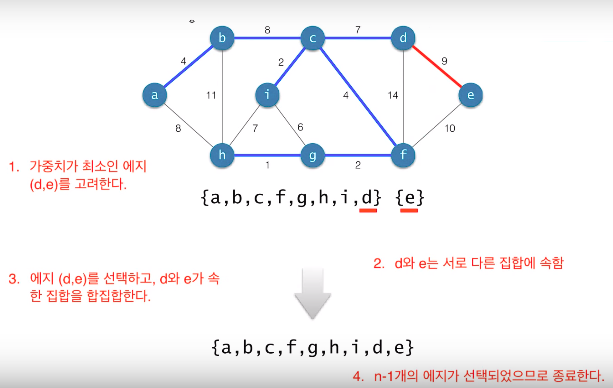
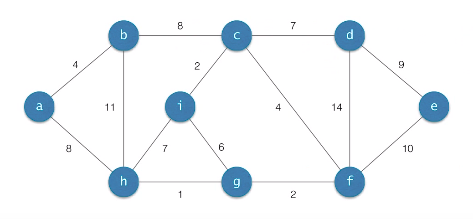
Kruskal의 알고리즘

• 시간복잡도

  

인프런의 영리한 프로그래밍을 위한 알고리즘 강좌를 보고 작성한 문서입니다.

Kruskal의 알고리즘

• 에지들을 가중치의 오름차순으로 정렬한다.

• 에지들을 그 순서대로 하나씩 선택해간다. 단, 이미 선택된 에지들과 사이클(cycle)을 형성하면 선택하지 않는다.

• n-1개의 에지가 선택되면 종료한다.

왜 MST가 찾아지는가?

• Kruskal의 알고리즘의 임의의 한 단계를 생각해보자.

• A를 현재까지 알고리즘이 선택한 에지의 집합이라고 하고, A를 포함하는 MST가 존재한다고 가정하자.

  

사이클 검사

• 초기 상태 : 선택된 에지 없음

• 각각의 연결요소를 하나의 집합으로 표현

  

  

  

  (가중치 순으로 반복)

  

  

  (반복)

  

Kruskal의 알고리즘

인프런의 영리한 프로그래밍을 위한 알고리즘 강좌를 보고 작성한 문서입니다.

최소신장트리(Minimum Spanning Tree)

• 입력 : n개의 도시, 도시와 도시를 연결하는 비용

• 문제 : 최소의 비용으로 모든 도시들이 서로 연결되게 한다.

  

  해가 유일하지는 않음

• 무방향 가중치 그래프 G = ( V, E )

• 각 에지 (u, V ) ∈ E 에 대해서 가중치 w( u, V )

  

왜 트리라고 부르나?

• 싸이클이 없는 연결된(connected) 무방향 그래프를 트리라고 부른다.

• MST 문제의 답은 항상 트리가 된다. 왜?

  

  노드가 n개인 트리는 항상 n-1개의 에지를 가짐

Generic MST 알고리즘

• 어떤 MST의 부분집합 A에 대해서 AU{(u,V)}도 역시 어떤 MST의 부분 집합이 될 경우 에지 (u, V)는 A에 대해서 안전하다(safe)고 한다.

• Generic MST 알고리즘:

  1. 처음에는 A=∅ 이다.
  2. 집합 A에 대해서 안전한 에지를 하나 찾은 후 이것을 A에 더한다.
  3. 에지의 개수가 n-1개가 될 때까지 2번을 반복한다.

안전한 에지 찾기

• 그래프의 정점들을 두 개의 집합 S와 V-S로 분할한 것을 컷(cut) (S, V-S)라고 부른다.

• 에지 (u, V)에 대해서 u ∈ V-S일 때 에지 (u, V)는 컷 (S, V-S)를 cross한다고 말한다.

• 에지들의 부분집합 A에 속한 어떤 에지고 컷 (S, V-S)를 cross하지 않을 때 컷 (S, V-S)는 A를 존중한다(respect)고 말한다.

  

• A가 어떤 MST의 부분집합이고, (S, V-S)는 A를 존중하는 컷이라고 하자. 이 컷을 cross하는 에지들 중 가장 가중치가 작은 에지 (u, V)는 A에 대해서 안전하다.

인프런의 영리한 프로그래밍을 위한 알고리즘 강좌를 보고 작성한 문서입니다.

DAG (Directed Acyclic Graph)

• DAG는 방향 사이클(directed cycle)이 없는 방향 그래프.

• 예: 작업들의 우선순위

  

위상정렬(topological ordering)

• DAG에서 노드들의 순서화 V1, V2,…,Vn, 단, 모든 에지 (Vi, Vj)에 대해서 i < j가 되도록.

  

위상정렬 알고리즘 1

topologicalsort1 ( G )
{
  for <- 1 to n {
    진입간선이 없는 임의의 정점 u를 선택한다;
    A[ i ] <- u;
    정점 u와 u의 진출간선을 모두 제거한다;
  }
  배열 A[ 1...n ]에는 정점들을 위상정렬되어 있다
}

수행시간 : θ( n + m )

예)

위상정렬 알고리즘 2

topologicalSort2 ( G )
{
  for each v ∈ V
    visited[V] <- NO;
  make an empty linked list R;
  for each v ∈ V -> 정점의 순서는 상관없음
    if ( visited[V] = NO ) then
      DFS-TS(v, R);
}

DFS-TS ( v, R )
{
  visited[v] <- YES;
  for each x adjacent to v do
    if (visited[x] = NO ) then
      DFS-TS( x, R );
  add v at the front of the linked list R;
}

• 알고리즘이 끝나면 연결 리스트 R에는 정점들이 위상정렬된 순서로 매달려 있다.

  수행시간 : θ( n + m )

예)

인프런의 영리한 프로그래밍을 위한 알고리즘 강좌를 보고 작성한 문서입니다.

깊이우선순회 (DFS)

1. 출발점 s에서 시작한다.

2. 현재 노드를 visited로 mark하고 인접한 노드들 중 unvisited 노드가 존재하면 그 노드로 간다.

3. 2번을 계속 반복한다.

4. 만약 unvisited인 노드가 존재하지 않는 동안 계속해서 직전 노드로 되돌아간다.

5. 다시 2번을 반복한다.

6. 시작노드 s로 돌아오고 더 이상 갈 곳이 없으면 종료한다.

다른 예)

DFS 깊이우선탐색

DFS (G, V)  
  visited[v] <- YES;
  for each node adjacent to u do
    if visited[u] = NO then
      DFS(G, u);
  end.
end.  

• 그래프가 disconnected이거나 혹은 방향 그래프라면 DFS에 의해서 모든 노드가 방문되지 않을 수도 있음

• DFS를 반복하여 모든 노드 방문

  DFS-ALL(G)
  {
    for each v ∈ V
      visited[V] <- NO;
    for each V ∈ V
      if ( visited[V] = NO ) then
        DFS(G, V);
  }
  

  시간복잡도: O(n+m)