인프런의 영리한 프로그래밍을 위한 알고리즘 강좌를 보고 작성한 문서입니다.

Floyd Warshall 알고리즘

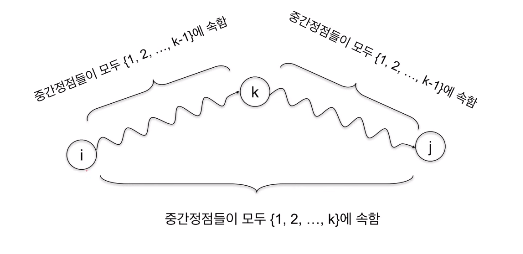
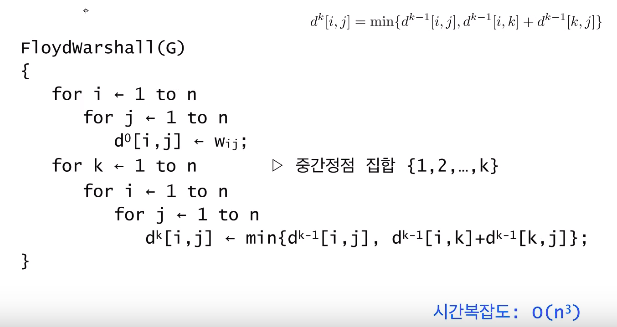
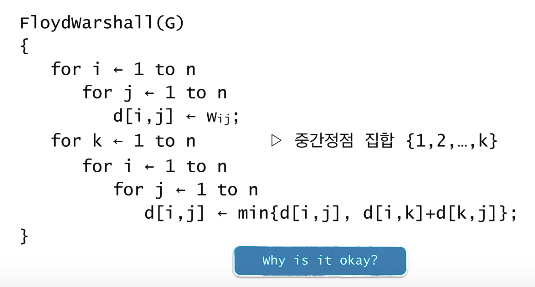
경로 찾기

경로 출력하기

• s에서 t까지 가는 경로가 존재한다는 가정하에 최단경로상의 중간노드들(s와 t자신은 제외)을 출력한다.

  

인프런의 영리한 프로그래밍을 위한 알고리즘 강좌를 보고 작성한 문서입니다.

Bellman-Ford 알고리즘

Worst Scenario

Dijkstra 알고리즘

Dijkstra 알고리즘

수도코드

시간 복잡도를 낮추는 방법

• 이진힙을 사용

시간복잡도

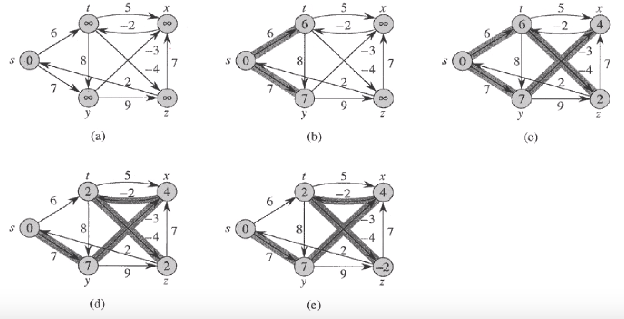
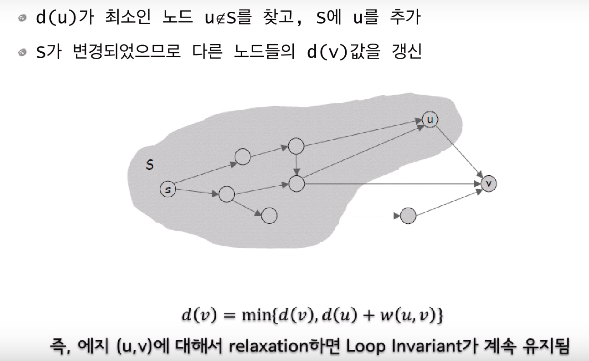
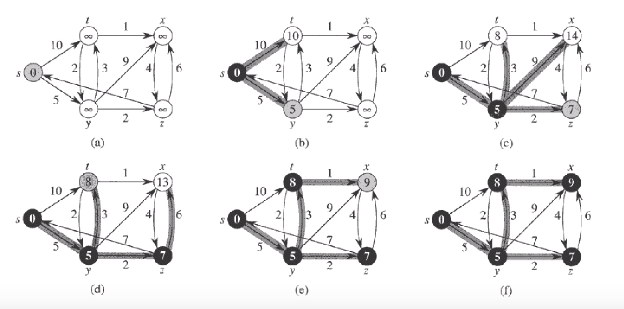
• prim의 알고리즘과 동일함

• 우선순위 큐를 사용하지 않고 단순하게 구현할 경우 O(n^2)

• 이진힙을 우선순위 큐로 사용할 경우 O(nlongn + mlogn)

• Fibonacci Heap을 사용하면 O(nlogn+m)에 구현가능

인프런의 영리한 프로그래밍을 위한 알고리즘 강좌를 보고 작성한 문서입니다.

최단경로

최단경로문제의 유형

• Single-source :

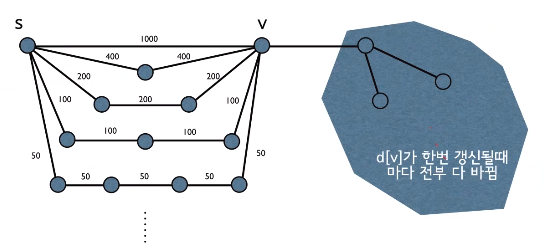
  • 하나의 출발 노드 s로부터 다른 모든 노드까지의 최단 경로를 찾아라.

  • 예 Dijkstra의 알고리즘

• Single-destination :

  • 모든 노드로부터 하나의 목적지 노드까지의 최단 경로를 찾아라.

  • Single-source 문제와 동일

• Single-pair :

  • 주어진 하나의 출발 노드 s로 부터 하나의 목적지 노드 t까지의 최단 경로를 찾아라

  • 최악의 경우 시간복잡도에서 Single-source 문제보다 나은 알고리즘이 없음

• All-pairs :
  • 모든 노드 쌍에 대해서 최단 경로를 찾아라.

최단경로와 음수 가중치

• 알고리즘에 따라 음수 가중치가 있어도 작동하는 경우도 있고 그렇지 않은 경우도 있음

  

최단경로의 기본 특성

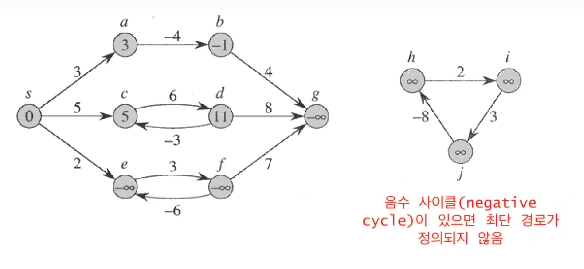
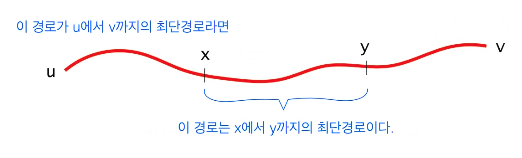
• 최단 경로의 어떤 부분경로도 역시 최단 경로이다.

  

• 최단 경로는 사이클을 포함하지 않는다.(음수 사이크링 없다는 가정하에서)

Single-source 최단경로문제

기본 연산: Relaxation

Single-source 최단경로

기본 알고리즘

즉, n-1번의 반복으로 충분하다.

Bellman-Ford 알고리즘

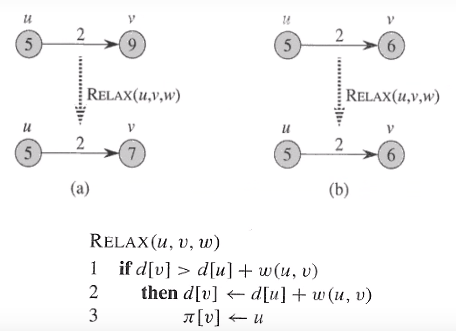
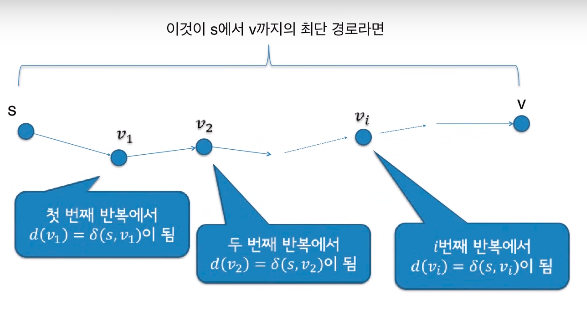
인프런의 영리한 프로그래밍을 위한 알고리즘 강좌를 보고 작성한 문서입니다.

Prim의 알고리즘

• 임의의 노드를 출발노드로 선택

• 출발 노드를 포함하는 트리를 점점 키워 감.

• 매 단계에서 이미 트리에 포함된 노드와 포함되지 않은 노드를 연결하는 에지들 중 가장 가중치가 작은 에지를 선택

  

예)

왜 MST가 찾아지는가?

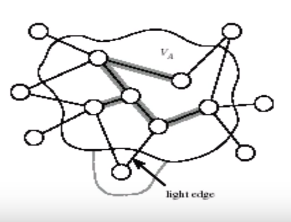
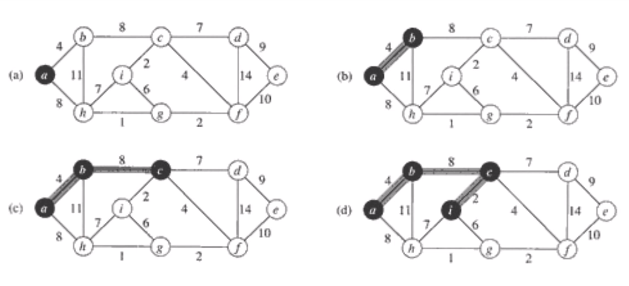
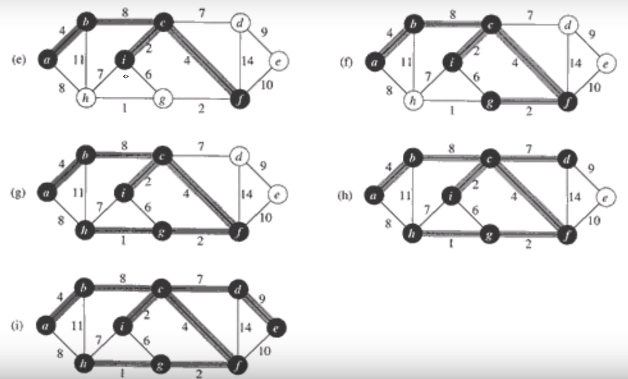
• prim의 알고리즘의 임의의 한 단계를 생각해보자.

• A를 현재까지 알고리즘이 선택한 에지의 집합이라고 하고, A를 포함하는 MST가 존재한다고 가정하자.

  

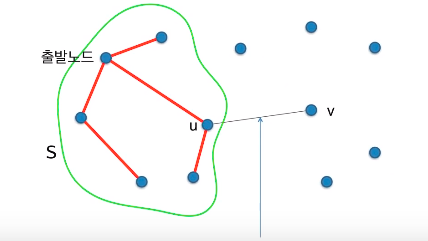
  출발 노드에 이미 연결된 노드와 그렇지 않은 노드를 연결하는 에지들 중 lightest edge

가중치가 최소인 에지 찾기

가중치가 최소인 에지 찾기

• 가중치가 최소인 에지를 찾는 대신 key값이 최소인 노드를 찾는다.

  

  

  

Prim의 알고리즘

Key값이 최소인 노드 찾기

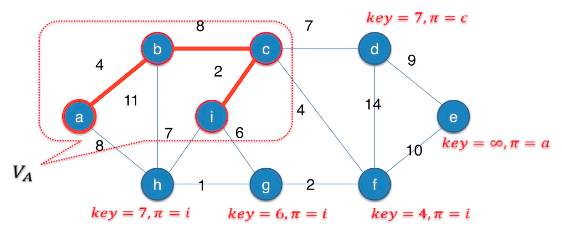
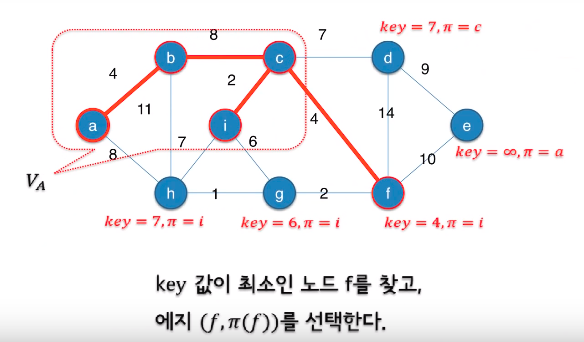
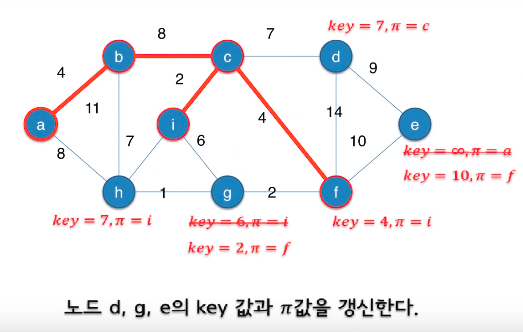
• 최소 우선순위 큐를 사용

  • V - VA에 속한 노드들을 저장

  • Extract-Min : Key값이 최소인 노드를 삭제하고 반환

  

Prim의 알고리즘 : 시간복잡도

• 이진 힙(binary heap)을 사용하여 우선순위 큐를 구현한 경우

• while loop :

  • n번의 Extract-Min 연산 : O(nlongn)

  • m번의 Decrease-Key 연산 : O(mlongn)

• 따라서 시간복잡도 : O(nlong + mlogn) = O(mlogn)

• 우선순위 큐를 사용하지 않고 단순하게 구현할 경우 : O(n^2)

• Fibonacci 힙을 사용하여 O(m+nlogn)에 구현 가능 [Fredman-Tarjan 1984]

호이스팅(hoisting)이란??

호이스팅의 뜻은 네이버 백과사전을 보면

hoist : (흔히 밧줄이나 장비를 이용하여) 들어[끌어]올리다

즉, 끌어 올리다 입니다.

단어의 뜻처럼 호이스팅은 변수의 선언을 위로 끌어올립니다.

console.log(foo);
var foo = "foo";
console.log(foo);

출력 :

undefined
foo

위와 같이 동작하는 원리는 자바스크립트 엔진에 의해서

var foo;
console.log(foo);
foo = "foo";
console.log(foo);

이와 같은 코드로 실행이 됩니다. (위의 코드를 보면 출력 결과가 납득이 될 겁니다.)

단, 분명히 var foo = "foo"; 로 작성했는데 foo가 출력 안된 점에서 의아해하실 수도 있습니다.

그 원인은 위에서도 말했다시피 변수의 선언을 위로 올리는 것이지 = "foo"에 해당하는 할당 구문은 위로 올라가지 않습니다.

Scope를 신경쓰자!!

한가지 더 조심해야 할 점은 선언된 해당 Scope에서 최상위에 위치한다는 점입니다.

console.log(foo);
var foo = "foo";
console.log(foo);

goo();

function goo(){
  console.log(foo);
  var foo = "goo";
  console.log(foo);
}

출력 :

undefined
foo
undefined
goo

위와 같이 실제 어떤 식으로 실행되는지 보면

var foo;
console.log(foo);
foo = "foo";
console.log(foo);

goo();

function goo(){
  var foo;
  console.log(foo);
  foo = "goo";
  console.log(foo);
}

이렇게 됩니다.

근데 goo()가 어떻게 정상적으로 실행됐는지 헷갈리는 분들도 있겠죠???

바로 아래서 설명을 이어나가도록 하겠습니다.

함수의 호이스팅

이번엔 함수의 선언을 보죠.

foo();

function foo(){
  console.log("hi!!");
}

출력 :

hi!!

이것도 위와 같이

function foo(){
  console.log("hi!!");
}

foo();

이렇게 실행됩니다.

그래서 위에 있는 goo()가 제대로 실행될 수 있었던 겁니다.

var foo = function(){} 같은 경우는??

foo();

var foo = function(){
  console.log("hi!!");
}

이렇게 작성하면 에러가 납니다.

(TypeError: foo is not a function)

원인은 맨 처음 말씀드린 것처럼 선언이 위로 올라가기 때문에

var foo;

foo();

foo = function(){
  console.log("hi!!");
}

이와 같은 형태가 됩니다.

()는 함수를 실행시킬 때 사용하죠. 하지만 foo에는 아직 함수가 할당되어 있지 않습니다. 그렇기 때문에 에러가 납니다.

좀더 정확히는

“함수 표현식”으로 정의된 함수는 호이스트 되지 않습니다. “함수 선언문”만 호이스트 됩니다.

• 함수 선언식

  function 함수명() {
    ...
  }
  

• 함수 표현식

  var 함수명 = function () {
    ...
  };
  

보면 함수 표현식의 경우 var 함수명에 함수를 할당해 주는 형태입니다.

그럼 위에서 설명 한 것처럼 할당은 그 자리에 남아 있을 테니 구현식, 표현식이라는 단어를 떠나서 생각해봐도 호이스팅이 어떻게 일어날지 유추를 해 볼 수 있습니다.

마치며

호이스팅(hoisting)은 선언되어 있는 변수 및 함수가 해당 Scope에서 최상위에 위치하는 걸 뜻합니다.

즉, 호이스팅을 알기 위해 중요한 것은 선언과 할당의 구분과 끌어 올려지는 위치에 관여하는 scope입니다.