화이트 코스때 스프링부트로 구현 했던 작업물을 JSP, Servlet을 이용하여 구현.
jstl 사용하여 JSP에서 java코드 제거
JDBC를 활용한 데이터베이스 연동(MySQL)
알고리즘 강의의 기본적인 정렬에 대해 공부했다. (포스팅)
JSP, Servlet으로 웹애플리케이션 구현하기
알고리즘 강의 듣기
추석 연휴동안 경기창조혁신센터가 쉰다. 카페에 가서 공부하자.
AWS 서버리스(Serverless) 워크샵 시리즈 2017 - 1주차를 참석하여 웹 리소스 호스팅, 사용자 인증 관리, RESTful API 사용법에 대한 방법을 학습했다.
Amazon S3
Cognito
API Gateway
Lambda
DynamoDb
공부하느라 못(혹은 안) 만나고 있던 친구들을 근 두달만에 만나서 다른 공부는 못했다..
AWS의 워크샵이 하나하나 상세히 알려주는 수업은 아니고, 간단히 따라해보는 형식의 수업이였다. AWS의 몇몇 기능들을 쓸려고 했을때(대표적으로 S3) 너무나 많은 옵션들이나 탭이 존재해서 간단한 작업을 해보고 싶어서 쉽게 접근을 못했었는데 오늘 좋은 기회가 된거 같다.
간단하게 따라서 해봄으로써 일단은 만들어 볼수는 있게 되었고 무엇을, 어떻게 되는건지는 추가적으로 공부할 여지가 생긴거 같다. 정말 좋은 자리였던거 같다. 총 4번의 워크샵 중 3개만 신청이 완료됐고 한개는 대기자인데 가능하다면 네번 다 참석하고 싶다.
다들 근처에 살다보니 일주일에 두번씩은 본다. 그때마다 아무말 없이 안가다가 두달만에 만났는데, “자주 좀 보자”, “얼굴보기 힘들다.” 이런 말을 안한다. 거기다 어제 봤다는 듯이 어색함이 없다. 정말 좋은 친구들이다.
JSP, Servlet으로 웹애플리케이션 구현하기
알고리즘 강의 듣기
인프런의 영리한 프로그래밍을 위한 알고리즘 강좌를 보고 작성한 문서입니다.
{a,b,c,d,e,f}의 모든 부분집합을 나열하려면
a를 제외한 {b,c,d,e,f}의 모든 부분집합들을 나열하고
{b,c,d,e,f}의 모든 부분집합에 {a}를 추가한 집합들을 나열한다.
{b,c,d,e,f}의 모든 부분집합에 {a}를 추가한 집합들을 나열하려면
{c,d,e,f}의 모든 부분집합들에 {a}를 추가한 집합들을 나열하고
{c,d,e,f}의 모든 부분집합에 {a,b}를 추가한 집합들을 나열한다.
{c,d,e,f}의 모든 부분집합에 {a}를 추가한 집합들을 나열하려면
{d,e,f}의 모든 부분집합들에 {a}를 추가한 집합들을 나열하고
{d,e,f}의 모든 부분집합에 {a,c}를 추가한 집합들을 나열한다.
powerSet(S)
if S is an empty set
print nothing;
else
let t be the first element of S;
find all subsets of S-{t} by calling powerSet(S-{t});
print the subsets;
print the subsets with adding t;
위의 코드는 약간의 오류가 있다. 현재의 요구사항은 모든 부분집합을 출력하기만 하는 것인데, 현재는 찾은 부분집합들의 전체를 return으로 받아와서 출력함으로써 필요없는 메모리를 사용하게 된다.
그래서 아래처럼 return 없이 내부에서 출력하게 바꾼다.
powerSet(P, S)
if S is an empty set
print P;
else
let t be the first element of S;
powerSet(P, S-{t});
powerSet(P U {t}, S-{t});
S의 멱집합을 구한 후 각각에 집합 P를 합집합하여 출력하라
recursion 함수가 두 개의 집합을 매개변수로 받도록 설계해야 한다는 의미이다. 두 번째 집합의 모든 부분집합들에 첫번째 집합을 합집합하여 출력한다.
private static char data[] = {'a','b','c','d','e','f'};
private static int n = data.length;
private static boolean[] include = new boolean[n];
public static void powerSet(int k){
if (k == n){
for(int i = 0; i < n; i++ ){
if(include[i]){
System.out.print(data[i] + " ");
}
}
System.out.println();
return;
}
include[k] = false;
powerSet(k+1);
include[k] = true;
powerSet(k+1);
}
data[k], … , data[n-1]의 멱집합을 구한 후 각각에 include[i]=true, i=0, …, k-1인 원소를 추가하여 출력하라.
처음 이 함수를 호출할 때는 powerSet(0)로 호출한다. 즉 P는 공집합이고 S는 전체집합이다.
(그림에 include와 exclude가 잘못 되어있다. 다 반대)
해를 찾기 위해 탐색할 필요가 있는 모든 후보들을 포함하는 트리
트리의 모든 노드들을 방문하면 해를 찾을 수 있다.
루트에서 출발하여 체계적으로 모든 노드를 방문하는 절차를 기술한다.
화이트 코스때 스프링부트로 구현 했던 작업물을 JSP, Servlet을 이용하여 구현.
회원가입, 로그인 기능 구현
MVC 모델을 이용하여 View단은 JSP로, Controller단은 Servlet을 이용하여 구현하기 시작.
알고리즘 강의의 순환을 이용하여 멱집합을 공부했다. (포스팅)
AWS 서버리스(Serverless) 워크샵 시리즈 2017 참석
JSP, Servlet으로 웹애플리케이션 구현하기
알고리즘 강의 듣기
인프런의 영리한 프로그래밍을 위한 알고리즘 강좌를 보고 작성한 문서입니다.
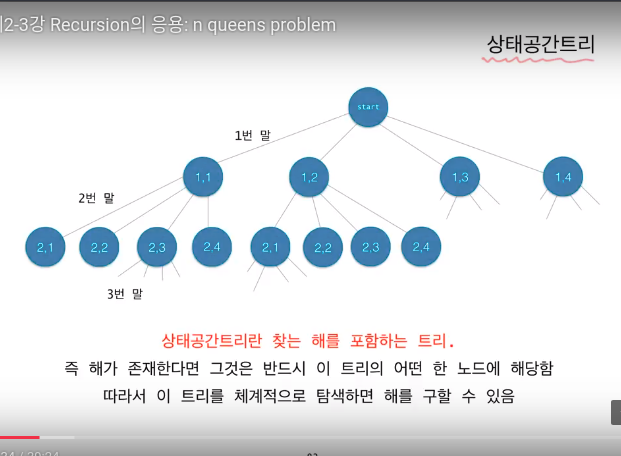
상태공간 트리의 모든 노드를 탐색해야 하는 것은 아니다.
내가 해온 과정을 돌아간다. 결정들을 하다가 막다른 결과에 도달하면 가장 최근에 내린 결정을 번복하고 다시 한다.
상태공간 트리를 깊이 우선 방식으로 탐색하여 해를 찾는 알고리즘을 만한다.
recursion
일반적으로 recursion으로 구현하는게 더 쉽다.
stack
수도코드를 작성한다. (Design Recursion)
return-type queens(arguments){
if non-promisiong
report failur and return;
else if success
report answer and return;
else
visit children recursively;
}
매개변수 level은 현재 노드의 행을 표현하고, 1번에서 level 말이 어디에 놓였는지는 전역변수 배열 cols로 표현하자.
cols[i] = j는 i번 말이 (i행, j열)에 놓였음을 의미한다.
int[] cols = new int[N+1];
return-type queens(int level){
if non-promisiong
report failur and return;
else if success
report answer and return;
else
visit children recursively;
}
queens 메소드의 매개변수와 리턴타입 결정.
int[] cols = new int[N+1];
boolean queens(int level){
if non-promisiong
report failur and return;
else if success
report answer and return;
else
visit children recursively;
}
이전 행과 비교하여 놓을수 없는 곳인지 확인하는 메소드인 promising를 통해(아직 미구현) 놓을 수 없는 곳이면 false를 리턴하게 한다.
int[] cols = new int[N+1];
boolean queens(int level){
if(!promising(level)){
return false;
}
else if success
report answer and return;
else
visit children recursively;
}
성공 했을때는 true를 리턴하게 하고, 순환적으로 다음 행도 queens 메소드가 호출 되게 구현.
int[] cols = new int[N+1];
boolean queens(int level){
if(!promising(level)){
return false;
}
else if(level == N){
return true;
}
for(int i=1; i <= N; i++){
cols[level + 1] = i;
if(queens(level+1)){
return true;
}
}
return false;
}
promising메소드를 구현한다. 이전에 놓은 말들과 이번 행의 말이 같은 열이면 false를 리턴.
boolean promising(int level){
for(int i = 1; i < level; i++){
if( cols[i] == cols[level]){
return false;
} else if on the same diagonal{
return false;
}
}
return true;
}
동일한 대각선에 있으면 false를 리턴하는 조건을 만든다.
|x - x’ | = | y - y’ |
두변의 길이가 같다면 동일 대각선이다.
boolean promising(int level){
for(int i = 1; i < level; i++){
if( cols[i] == cols[level]){
return false;
} else if(level-i==Math.abs(cols[level]-cols[i])){
return false;
}
}
return true;
}
앞서 만든 queens와 promising 메소드를 합친다.(추가적으로 출력 부분도 구현)
int[] cols = new int[N+1];
boolean queens(int level){
if(!promising(level)){
return false;
}
else if(level == N){
for(int i = 1; i <= N; i++){
System.out.println("(" + i + ", " + cols[i] + ")");
}
return true;
}
for(int i=1; i <= N; i++){
cols[level + 1] = i;
if(queens(level+1)){
return true;
}
}
return false;
}
boolean promising(int level){
for(int i = 1; i < level; i++){
if( cols[i] == cols[level]){
return false;
} else if(level-i==Math.abs(cols[level]-cols[i])){
return false;
}
}
return true;
}