인프런의 영리한 프로그래밍을 위한 알고리즘 강좌를 보고 작성한 문서입니다.
이진검색트리
-
여러 개의 키(key)를 저장
-
다음과 같은 연산들을 지원하는 자료구조
-
INSERT - 새로운 키의 삽입
-
SEARCH - 키 탐색
-
DELETE - 키의 삭제
-
-
예: 심볼 테이블
다양한 방법들
-
정렬된 혹은 정렬되지 않은 배열 혹은 연결 리스트를 사용할 경우 INSET, SEARCH, DELETE 중 적어도 하나는 O(n)
-
이진탐색트리(Binary Search Tree), 레드-블랙 트리, AVL-트리 등의 트리에 기반한 구조들
-
Direct Address Table, 해쉬 테이블 등
검색트리
-
Dynamic set을 트리의 형태로 구현
-
일반적으로 SEARCH, INSERT, DELETE 연산이 트리의 높이(height)에 비례하는 시간복잡도를 가짐
-
이진검색트리(Binary Search Tree), 레드-블랙 트리(red-black tree), B-트리 등
이진검색트리(BST)
-
이진 트리이면서
-
각 노드에 하나의 키를 저장
-
각 노드 v에 대해서 그 노드의 왼쪽 부트리(subtree)에 있는 키들은 key[v]보다 작거나 같고, 오른쪽 부트리에 있는 값은 크거나 같다.
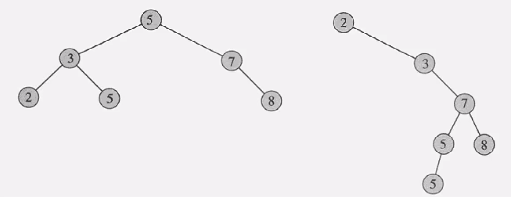
BST의 예
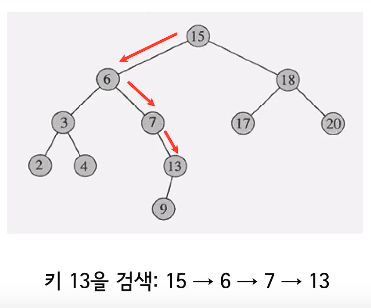
BST Search
수도코드
Recusive Version
TREE-SEARCH(x,k)
1 if x = NIL or k = key[x]
2 then return x
3 if k < key[x]
4 then return TREE-SEARCH(left[x],k)
5 else return TREE-SEARCH(right[x],k)
Iterative Version
ITERATIVE-TREE-SEARCH(x,k)
1 while x != NIL and k != key[x]
2 do if k < key[x]
3 then x <- left[x]
4 else x <- right[x]
5 return x