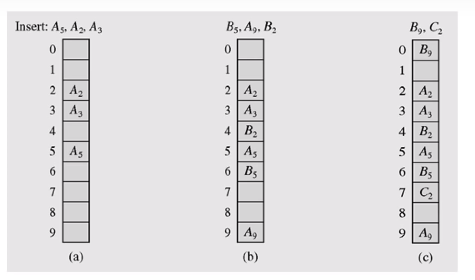
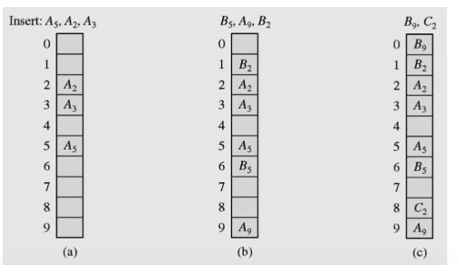
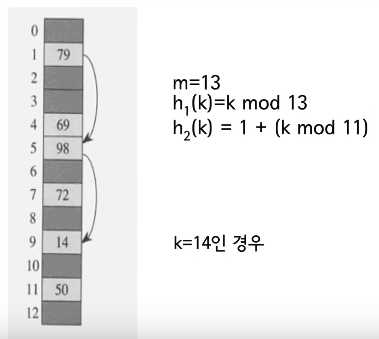
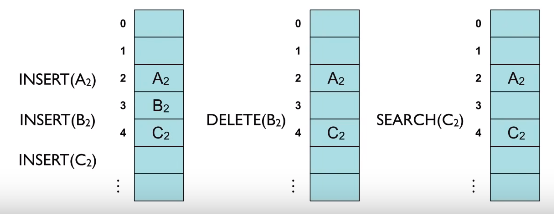
인프런의 영리한 프로그래밍을 위한 알고리즘 강좌를 보고 작성한 문서입니다.
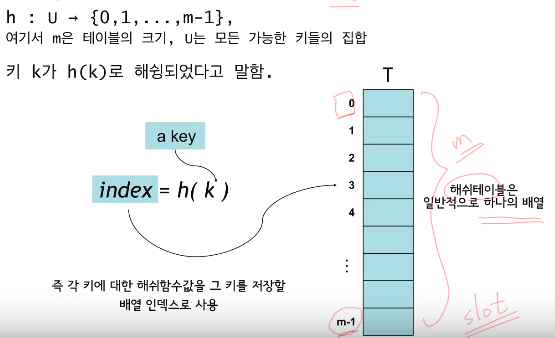
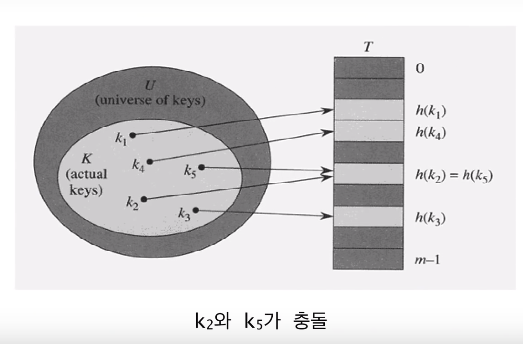
좋은 해쉬 함수란?
-
현실에서는 키들이 랜덤하지 않음
-
만약 키들으 티오계적 분포에 대해 알고 있담녀 이를 이용해서 해쉬 함수를 고안하는 것이 가능하겠지만 현실적으로 어려움
-
키들이 어떤 특정한 (가시적인) 패턴을 가지더라도 해쉬함수값이 불규칙적이 되도록 하는게 바람직
- 해쉬함수값이 키의 특정 부분에 의해서만 결정되지 않아야 한다.(학번처럼 앞 부분이 많이 중복되는 경우 문제가 생길 수 있다.)
해쉬 함수
Division 기법
-
h(k) = k mod m
-
예: m = 20 and k = 91 => h(k) = 11
-
장점: 한번의 mod연산으로 계산. 따라서 빠름
-
단점: 어떤 m값에 대해서는 해쉬 함수값이 키값의 특정 부분에 의해서 결정되는 경우가 있음. 가령 m=2^p이면 키의 하위 p비트가 해쉬 함수값이 됨
multiplication 기법 :
-
0에서 1사이의 상수 A를 선택: 0<A<1
-
kA의 소수부분만을 택한다.
-
소수 부분에 m을 곱한 후 소수점 아래를 버린다.
예: m=8, word size = w = 5, k = 21
-
A = 13/32를 선택
-
kA = 21*13/32 = 273/32 = 8 + 17/32
-
m (kA mod 1) = 8 * 17/32 = 17/4 = 4.~
-
즉, h(21) = 4
Hash code in Java
-
Java의 Object 클래스는 hashCode() 메서드를 가짐. 따라서 모든 클래스는 hashCode() 메서드를 상속받는다. 이 메서드는 하나의 32비트 정수(음수 포함)를 반환한다.
-
만약 x.equals(y)이면 x.hashCode()==y.hashCode()이다. 하지만 역은 성립하지 않는다.
-
Object 클래스의 hashCode() 메서드는 객체의 메모리 주소를 반환하는 것으로 알려져 있음 (but it’s implementation-dependent)
-
필요에 따라 각 클래스마다 이 메서드를 override하여 사용한다.
- 예) Integer 클래스는 정수값을 hashCode로 사용
해쉬함수의 예: hashCode() for Strings in Java
public final class String
{
private final char[] s;
...
public int hashCode()
{
int hash = 0;
for ( int i = 0; i < length(); i++)
hash = s[i] + (31 * hash);
return hash;
}
}
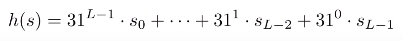
사용자 정의 클래스의 예
모든 멤버들을 사용하여 hashCode를 생성한다.
public class Record
{
private String name;
private int id;
private double value;
...
public int hashCode() {
int hash = 17; //nonzero constant, 프라임넘버로 꼭 17일 필요는 없다. 17은 일종의 가이드 라인
hash = 31*hash + name.hashCode();
hash = 31*hash + Integer.valueOf(id).hashCode();
hash = 31*hash + Double.valueOf(value).hashCode();
return hash;
}
}
hashCode와 hash 함수
-
Hash code: -2^31에서 2^31사이의 정수
-
Hash 함수: 0에서 M-1까지의 정수 (배열 인덱스)
private int hash(Key key) { //나머지 연산에서 음수면 문제가 생기니 "& 0x7fffffff"로 양수로 만든다. return (key.hashCode() & 0x7fffffff) % M; }
HashMap in Java
-
4장에서 다룬 TreeMap 클래스와 유사한 인터페이스를 제공(둘 다 java.util.Map 인터페이스를 구현)
-
내부적으로 하나의 배열을 해쉬 테이블로 사용
-
해쉬 함수는 24페이지의 것과 유사함
-
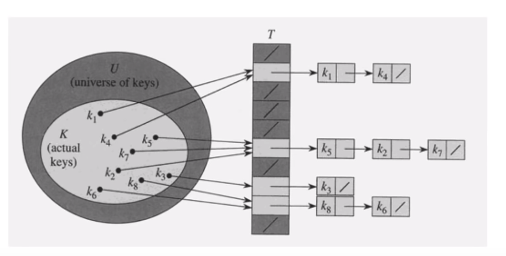
chaining으로 충돌 해결
-
load factor를 지정할 수 있음(0~1 사이의 실수)
-
저장된 키의 개수가 load factor를 초과하면 더 큰 배열을 할당하고 저장된 키들을 재배치(re-hashing)
HashSet in Java
HashSet<MyKey> set = new HashSet<MyKey>();
set.add(MyKey);
if (set.contains(theKey))
...
int k = set.size();
set.remove(theKey);
Iterator<MyKey> it = set.iterator();
while (it.hasNext()) {
MyKey key = it.next();
if (key.equals(aKey))
it.remove();
}