인프런의 영리한 프로그래밍을 위한 알고리즘 강좌를 보고 작성한 문서입니다.

선형시간 정렬 알고리즘

선형시간: O(n)

Counting Sort

• n개의 정수를 정렬하라. 단 모든 정수는 0에서 k사이의 정수이다.(사전지식)

• 예: n명의 학생들의 시험점수를 정렬하라. 단 모든 점수는 100이하의 양의 정수이다.

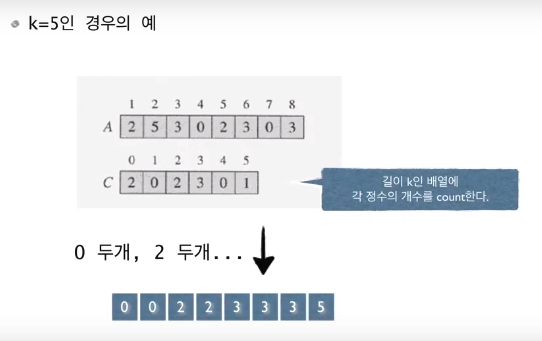
int A[n];
int C[k] = {0,};
for(int i = 1; i <= n; i++){
  C[A[i]]++;
}
for(int s = 1, i = 0; i <= k; i++){
  for(int j = 0; j < C[i]; j++){
    A[s++] = i;
  }
}

그러나 대부분의 경우 정렬할 key 값들은 레코드의 일부분이기 때문에 위와 같이 정렬할 데이터를 정수 값으로 보는 방식은 실제로 유용한 방식은 아니다.

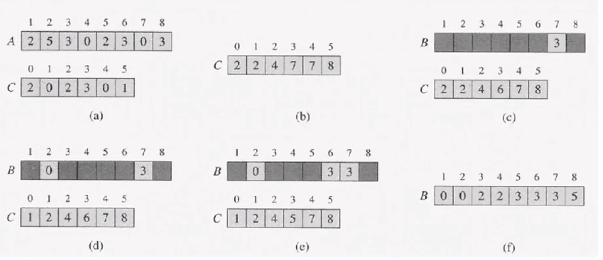
수도코드

Counting-Sort(A,B,k)
  for i <- 0 to k
    do C[i] <- 0
  for j <- 1 to length[A]
    do C[A[j]] <- C[A[j]] + 1
  > C[i] now contains the number of elements equal to i.
  for i <- 1 to k
    do C[i] <- C[i] + C[i - 1]
  > C[i] now contains the number of elements less than or equal to i.
  for j <- length[A] downto 1
    do B[C[A[j]]] <- A[j]
      C[A[j]] M- C[A[j]] - 1

• Θ(n+k), 또는 Θ(n) if k =O(n).

• k가 클 경우 비실용적

• Stable 정렬 알고리즘

  • “입력에 동일한 값이 있을때 입력에 먼저 나오는 값이 출력에서도 먼저 나온다.”
  • Counting정렬은 stable하다.