인프런의 영리한 프로그래밍을 위한 알고리즘 강좌를 보고 작성한 문서입니다.

레드블랙트리(Red-Black Tree)

BST의 경우 최악의 경우 극단적으로 밸런스가 무너진다.(계속 오른쪽 혹은 왼쪽의 자식만 있는 경우)

레드블랙 트리란?

• 이진탐색트리의 일종

• 균형잡힌 트리: 높이가 O(logn)

• SEARCH, INSERT, DELETE 연산을 최악의 경우에도 O(logn) 시간에 지원

• 각 노드는 하나의 키(key), 왼쪽자식(left), 오른쪽 자식(right), 그리고 부모노드(p)의 주소를 저장

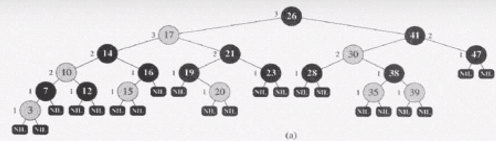
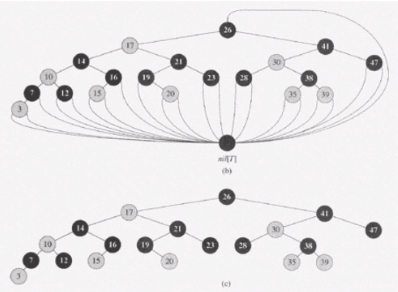
• 자식노드가 존재하지 않을 경우 NIL 노드라고 부르는 특수한 노드가 있다고 가정

• 따라서 모든 리프노드는 NIL노드

• 노드들은 내부노드와 NIL노드로 분류

• 실제 레드블랙 트리에서 NIL노드를 구현하진 않는다. 설명을 쉽게 하기 위한 용도

• 15, 20의 밑에 NIL노드가 있다고 가정

• 루트노드 위에도 NIL노드가 있다고 가정

• 그림 (b)의 가장 밑의 black 노드가 NIL노드

레드블랙 트리의 정의

1. 각 노드는 red 혹은 black이다.

2. 루트노드는 black이다.

3. 모든 리프노드(즉, NIL노드)는 black이다.

4. red노드의 자식노드들은 전부 black이다.(즉, red노드는 연속되어 등장하지 않는다.)

5. 모든 노드에 대해서 그 노드로부터 자손인 리프노드에 이르는 모든 경로에는 동일한 개수의 black노드가 존재한다.

#### 레드블랙 트리의 예)

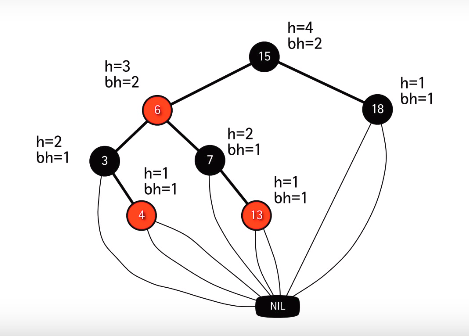
레드블랙 트리의 높이

• 노드 x의 높이 h(x)는 자신으로부터 리프노드까지의 가장 긴 경로에 포함된 에지의 개수이다.(현재 노드에서 NIL노드까지 가는데 필요한 가장 많은 선의 갯수)

• 노드 x의 블랙-높이 bh(x)는 x로부터 리프노드까지의 경로상의 블랙노드의 개수이다.(노드 x 자신은 불포함)

  

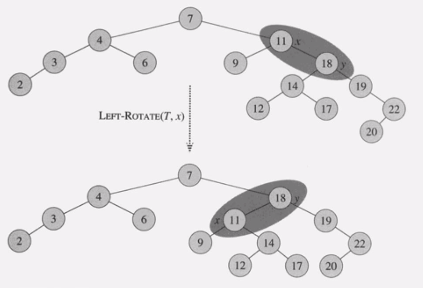
Left and Right Rotation

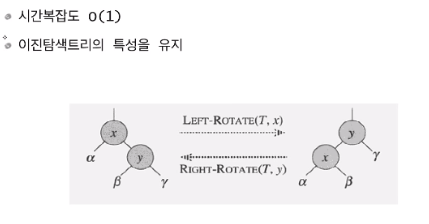
• 탐색은 기본적으로 BST의 알고리즘에서와 같으므로 삽입, 삭제만 공부 한다.

• Left and Right Rotation은 삽입, 삭제시 필요로 하는 기본적인 동작이다.

Left Rotation 수도코드

• y = right[x] != NIL이라고 가정

• 루트노드의 부모도 NIL이라고 가정

Left Rotation 수행시