인프런의 영리한 프로그래밍을 위한 알고리즘 강좌를 보고 작성한 문서입니다.

hashing

해쉬 테이블은 dynamic set을 구현하는 효과적인 방법의 하나

• 적절한 가정하에서 평균 탐색, 삽입, 삭제시간 O(1)

• 보통 최악의 경우 θ(n)

  

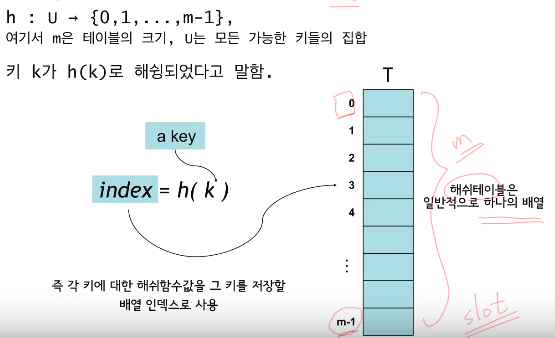
해쉬 함수(hash function) h를 사용하여 키 k를 T[h(k)]에 저장

• 모든 키들을 자연수라고 가정. 어떤 데이터든지 자연수로 해석하는 것이 가능

예)문자열

• ASCII 코드: C=67, L=76, R=82, S=83

해쉬 함수의 간단한 예:

• h(k) = k % m, 즉 key를 하나의 자연수로 해석한 후 테이블의 크기 m으로 나눈 나머지
• 항상 0~m-1 사이의 정수가 됨

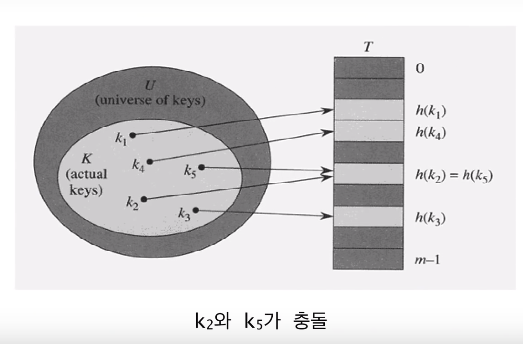
충돌

• 두 개 이상의 키가 동일한 위치로 해슁되는 경우

• 즉, 서로 다른 두 키 k1과 k2에 대해서 h(k1)=h(k2)인 상황

• 일반적으로 |U|»m이므로 항상 발생 가능 (즉 단사함수(일대일 함수)가 아님)

• 만약 |K|>m라면 당연히 발생, 여기서 K는 실제로 저장된 키들의 집합

• 충돌이 발생할 경우 대처 방법이 필요

• 대표적인 두 가지 충돌 해결 방법: chaining과 open addressing

  

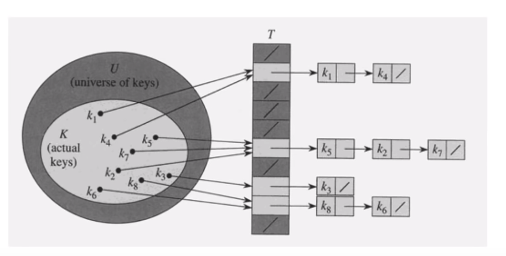
Chaining에 의한 충돌 해결

• 동일한 장소로 해슁된 모든 키들을 하나의 연결리스트(Linked List)로 저장

  

• 키의 삽입(Insertion)

  • 키 k를 리스트 T[h(k)]의 맨 앞에 삽입: 시간복잡도 O(1)

  • 중복된 키가 들어올 수 있고 중복 저장이 허용되지 않는다면 삽입시 리스트를 검색해야 함. 따라서 시간복잡도는 리스트의 길이에 비례

• 키의 검색(Search)

  • 리스트 T[h(k)]에서 순차검색

  • 시간복잡도는 키가 저장된 리스트의 길이에 비례

• 키의 삭제(Deletion)

  • 리스트 T[h(k)]로 부터 키를 검색 후 삭제

  • 일단 키를 검색해서 찾은 후에는 O(1)시간에 삭제 가능

최악의 경우

• 최악의 경우는 모든 키가 하나의 슬롯으로 해슁되는 경우

  • 길이가 n인 하나의 연결리스트가 만들어짐

  • 따라서 최악의 경우 탐색시간은 θ(n)+해쉬함수 계산시간

• 평균시간복잡도는 키들이 여러 슬롯에 얼마나 잘 분배되느냐에 의해서 결정

SUHA(Simple Uniform Hashing Assumption)

• 각각의 키가 모든 슬롯들에 균등한 확률로(equally likely) 독립적으로(independently) 해슁된다는 가정

  • 성능분석을 위해서 주로 하는 가정임
  • hash함수는 deterministic하므로 현실에서는 불가능
• Load factor a = n/m:
  • n: 테이블에 저장될 키의 개수
  • m: 해쉬테이블의 크기, 즉 연결리스트이 개수
  • 각 슬롯에 저장된 키의 평균 개수

• 연결리스트 T[j]의 길이를 nj라고 하면 E[nj] = a

• 만약 n=O(m)이면 평균검색시간은 O(1)