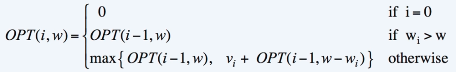인프런의 영리한 프로그래밍을 위한 알고리즘 강좌를 보고 작성한 문서입니다.

Knapsack Problem

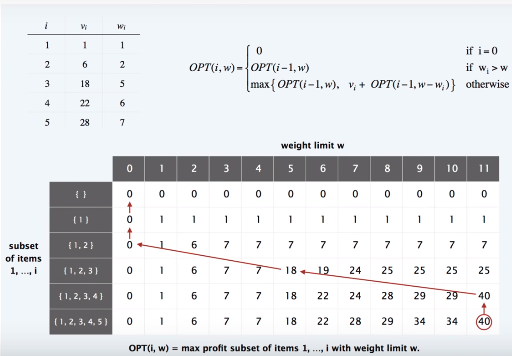
• n개의 아이템과 배낭

• 각각의 아이템은 무게 Wi와 가격 Vi를 가짐

• 배낭의 용량 W

• 목적: 배낭의 용량을 초과하지 않으면서 가격이 최대가 되는 부분집합

• 예 :

  

  • {1, 2, 5}는 가격의 합이 35

  • {3, 4}는 가격의 합이 40

  • {3, 5}는 46이지만 배낭의 용량을 초과함

Greedy

가격이 높은 것 부터 선택

무게가 가벼운 것부터 선택

단위 무게당 가격이 높은것 부터 선택

순환식

• OPT(i) : 아이템 1, 2, …, i로 얻을 수 있는 최대 이득

• 경우 1: 아이테[ㅁ i를 선택하지 않는 경우
  • OPT(i) = OPT( i - 1 )
• 경우 2: 아이템 i를 선택하는 경우
  • OPT(i) = ?

• OPT( i, W) : 배난 용량이 W일 때 아이템 1, 2, …, i로 얻을 수 있는 최대 이득

• 경우 1: 아이템 i를 선택하지 않는 경우
  • OPT( i, w ) OPT( i - 1, w )
• 경우 2: 아이템 i를 선택하는 경우
  • OPT(i) = OPT( i - 1, w - wi )

시간복잡도 O(nW)