인프런의 영리한 프로그래밍을 위한 알고리즘 강좌를 보고 작성한 문서입니다.

Matrix-Chain Multiplication

행렬의 곱셈

• pxq 행렬 A와 qxr 행렬 B 곱하기

  void product( int A[][], int B[][], int C[][] ) {
    for ( int i = 0; i < p; i++ ) {
      for (int j = 0; j < r; j++ ) {
        C[i][j] = 0;
        for ( int k = 0; k < q; k++)
          C[i][j] += A[i][k] * B[k][j];
      }
    }
  }
  

  곱셈연산의 횟수 = pqr

Matrix-Chain 곱하기

• 행렬 A는 10x100, B는 100x5, C는 5x50

• 세 행렬의 곱 ABC는 두 가지 방법으로 계산가능 (결합법칙이 성립)
  • (AB)C : 7,500번의 곱셈이 필요 ( 10x100x5 + 10x5x50 )
  • A(BC) : 75,000번의 곱셈이 필요 ( 100x5x50 + 10x100x50 )

• 즉 곱하는 순서에 따라서 연산량이 다름

• n개의 행렬의 곱 A1A2A3…An을 계산하는 최적의 순서는?

• 여기서 Ai는 Pk-1 x Pk 행렬이다.

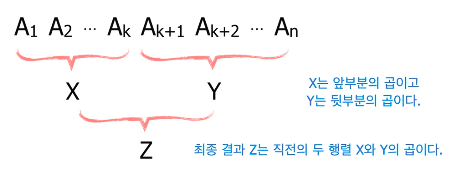
계산순서

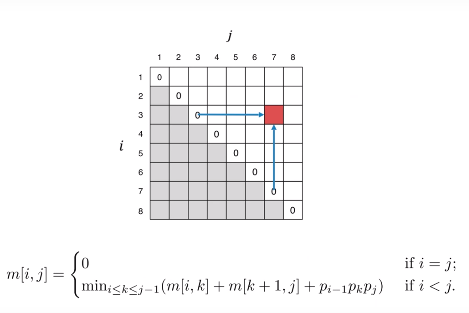
int matrixChain( int n ){
  for ( int i = 1; i <= n; i++ )
    m[i][i] = 0;

  for ( int r = 1; r <= n - 1; r++ ) {
    for ( int i = 1; i <= n -r; i++ ) {
      int j = i +r;
      m[i][j] = m[i+1][j] + p[i-1] * p[i] * p[j];
      for( int k = i + 1; k <= j - 1; k++ ) {
        if ( m[i][j] > m[i][k] + m[k+1][j] + p[i-1] * p[k] * p[j])
        m[i][j] = m[i][k] + m[k+1][j] + p[i-1] * p[k] * p[j];
      }
    }
  }
}

시간 복잡도 : θ^3