인프런의 영리한 프로그래밍을 위한 알고리즘 강좌를 보고 작성한 문서입니다.

행렬 경로 문제

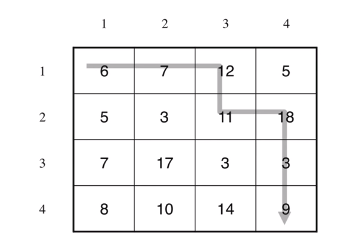
• 정수들이 저장된 nxn 행렬의 좌상단에서 우하단까지 이동한다. 단 오른쪽이나 아래쪽 방향으로만 이동할 수 있다.

• 방문한 칸에 있는 정수들의 합이 최소화되도록 하라.

  

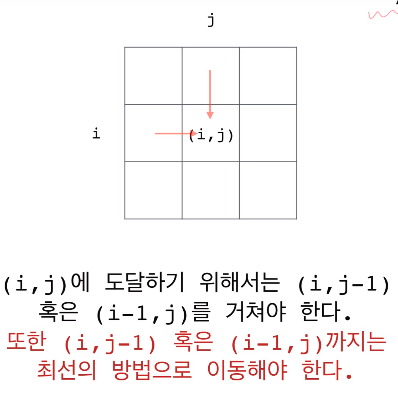
• Key Observation

  

• 순환식

  

• Recursive Algorithm

  int mat(int i, int j){
    if ( i == 1 && j == 1)
      return m[i][j];
    else if ( i == 1)
      return mat(1, j-1) + m[i][j];
    else if ( j == 1)
      return mat( i - 1, 1) + m[i][j];
    else
      return Math.min(mat( i - 1, j ), mat( i, j - 1 )) + m[i][j];
  }
  

• Memoization

  int mat(int i, int j){
    if ( L[i][j] != -1 ) return L[i][j];
    if ( i == 1 && j == 1 )
      L[i][j] = m[i][j];
    else if ( i == 1)
      L[i][j] = mat( 1, j-1 ) + m[i][j];
    else if ( j == 1 )
      L[i][j] = mat( i - 1 , 1 ) + m[i][j];
    else
      L[i][j] = Math.min( mat( i - 1 , j ), mat( i, j - 1 ) ) + m[i][j];
    return L[i][j];
  }
  

• Bottom-up

  

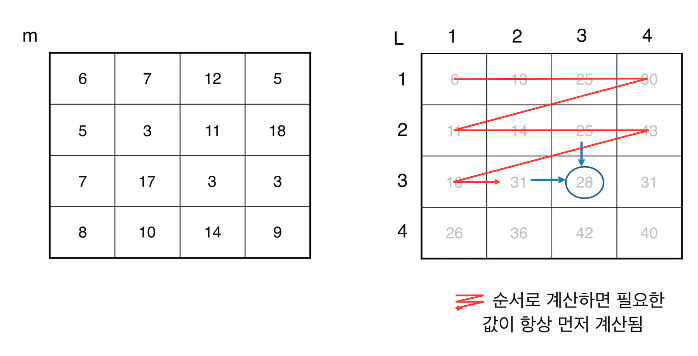
  int mat(){
    for ( int i = 1; i <= n; i++ ){
      for ( int j = 1; j <= n; j++ ){
        if ( i == 1 && j == 1 )
          L[i][j] = m[1][1];
        else if ( i == 1 )
          L[i][j] = m[i][j] + L[i][j-1];
        else if ( j == 1 )
          L[i][j] = m[i][j] + L[i-1][j];
        else
          L[i][j] =  m[i][j] + Math.min( L[i-1][j] , L[i][j-1] );
      }
    }
    return L[n][n];
  }
  

  • Common Trick

    // initialise L with L[0][j]=L[i][0]=무한대 for all i and j
    int mat(){
      for ( int i = 1; i <= n; i++ ){
        for (int j = 1; j <= n; j++ ){
          if ( i == 1 && j == 1 )
            L[i][j] = m[1][1];
          else
            L[i][j] =  m[i][j] + Math.min( L[i-1][j] , L[i][j-1] );
        }
      }
      return L[n][n];
    }
    

경로 구하기

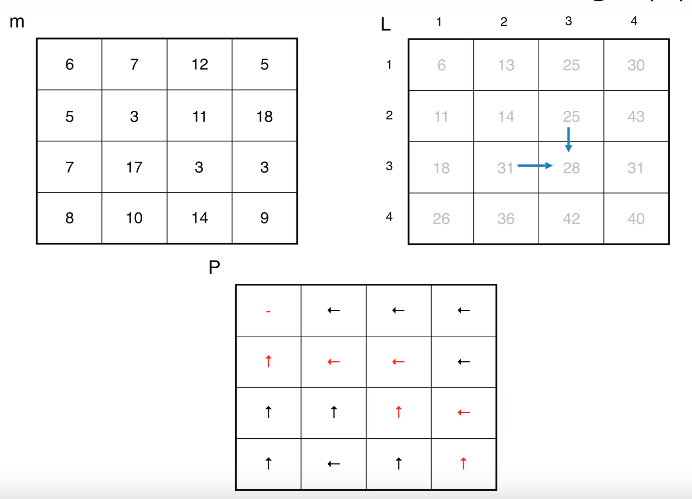
// initialise L with L[0][j]=L[i][0]=무한대 for all i and j
int mat(){
  for ( int i = 1; i <= n; i++ ){
    for ( int j = 1; j <= n; j++ ){
      if ( i == 1 && j == 1 ){
        L[i][j] = m[1][1];
        P[i][j] = '-';
      }
      else{
        if ( L[i-1][j] < L[i][j-1] ){
          L[i][j] = m[i][j] + L[i-1][j];
          P[i][j] = '←';
        }
        else{
          L[i][j] = m[i][j] + L[i][j-1];
          P[i][j] = '↑';
        }
      }
    }
  }
  return L[n][n];
}

출력

void printPath(){
  int i =n, j = n;
  while ( P[i][j] != '-' ) {
    print( i + " " + j );
    if ( P[i][j] == '←' )
      j = j-1;
    else
      i = i-1;
  }
  print( i + " " + j );
}

void printPathRecursive(int i, int j){
  int i = n, j = n;
  if( P[i][j] == '-' )
    print( i + " " + j );
  else{
    if ( P[i][j] == '←' )
      printPathRecursive( i, j - 1 );
    else
      printPathRecursive( i - 1 , j );
    print( i + " " + j );
  }
}