인프런의 영리한 프로그래밍을 위한 알고리즘 강좌를 보고 작성한 문서입니다.
Fibonacci Numbers
int fib(int n){
if (n==1 || n==2)
return 1;
else
return fib(n-2) + fib(n-1);
}
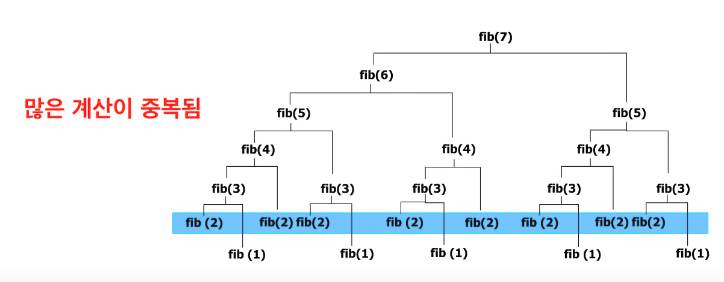
Memoization
int fib(int n){
if (n==1 || n==2)
return 1;
else if (f[n] > -1) // 배열 f가 -1으로 초기화되어 있다고 가정
return f[n]; // 즉 이미 계산된 값이라느 ㄴ의미
else {
f[n] = fib(n-2) + fib(n-1); //중간 계산 결과를 caching
return f[n];
}
}

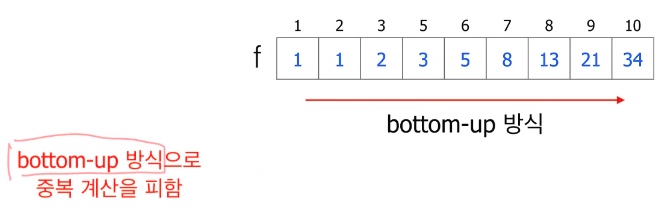
Bottom-up
int fib(int n){
f[1] = f[2] = 1;
for( int i=3; i<=n; i++)
f[n] = f[n-1] + f[n-2];
return f[n];
}
이항 계수(Binomial Coefficient)
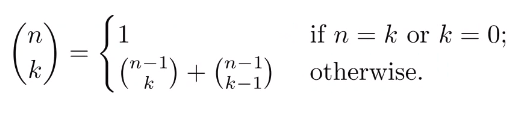
int binomial(int n, int k)
{
if ( n == k || k == 0)
return 1;
else
return binomial(n - 1, k) + binomial(n - 1, k - 1);
}
Memoization
int binomial(int n, int k){
if ( n == k || k == 0)
return 1;
else if (binom[n][k] > -1) //배열 binom이 -1로 초기화되어 있다고 가정
return binom[n][k];
else {
binom[n][k] = binomial(n-1, k) + binomial(n-1, k-1);
return binom[n][k];
}
}
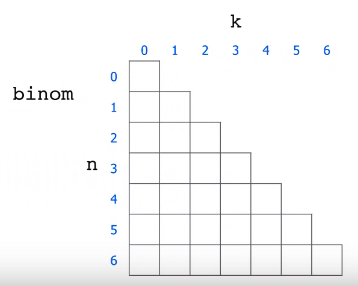
Bottom-up
int binomial(int n, int k){
for (int i=0; i<=n; i++){
for (int j=0; j<=k && j<=i; j++){
if (k==0 || n==k)
binom[i][j] = 1;
else
binom[i][j] = binom[i-1][j-1] + binom[i-1][j];
}
}
return binom[n][k];
}
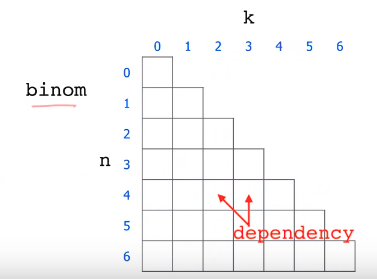
bottom-up 방식은 밑에부터 시작 한다는 뜻이 아니라 기본적인 부분부터 시작 한다는 것
Memoization vs. Dynamic Programming
-
순환식의 값을 계산하는 기법들이다.
-
둘 다 동적계획법의 일종으로 보기도 한다.
-
Memoization은 top-down방식이며, 실제로 피룡한 subproblem만을 푼다.
-
동적계획법은 bottom-up 방식이며, recursion에 수반되는 overhead가 없다.
