인프런의 영리한 프로그래밍을 위한 알고리즘 강좌를 보고 작성한 문서입니다.

Heap과 Heapsort

• 최악의 경우 시간복잡도 O(nlogn)

• Sorts in place - 추가 배열 불필요

• 이진 힙(binary heap) 자료구조를 사용

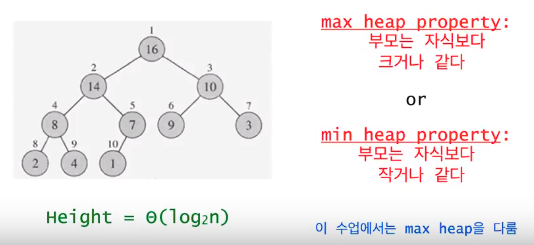
Heap은

• compleate binary tree이면서

• heap property를 만족해야한다.

Full v.s Complete Binary Trees

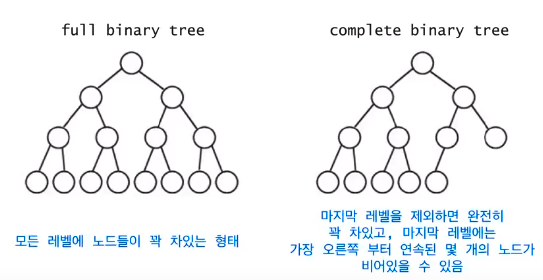
• Level

  부모로부터 몇칸 떨어져 있는가

힙은 일차원 배열로도 표현 가능하다

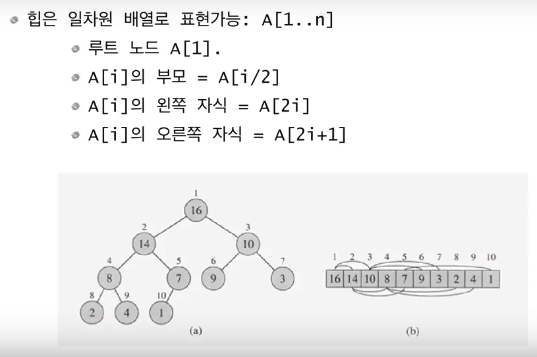
complete binary 트리이기때문에 인덱스를 통해 누구의 자식인지 알수 있다.

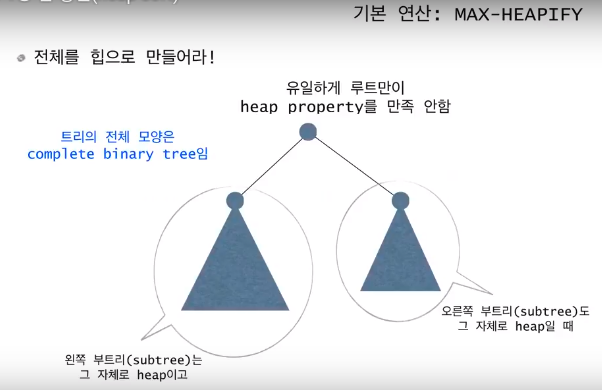
MAX-HEAPIFY

• 힙이라는 자료구조를 다루기 위한 필요한 기본연산.

• 전체가 heap을 만족하도록 각 노드들의 위치를 조정하는 과정.

• 자식의 값보다 부모의 값이 더 작으면 더 큰 자식과 부모를 바꿔가며 heap을 만족해 나간다.

수도코드

• recursive version

  MAX-HEAPIFY(A, i){
    if there is no child of A[i]{
      return;
    }
    k <- index of the biggest child of i;
    if A[i] >= A[k]{
      return;
    }
    exchange A[i] and A[k];
    MAX-HEAPIFY(A, k);
  }
  

  (root 노드에 대한 heapify는 MAX-HEAPIFY(1)을 호출하면 된다.)

• iterative version

  MAX=HEAPIFY(A, i){
    while A[i] has a child do{
      k <- index of the biggest child of i;
      if A[i] >= A[k]{
        return;
      }
      exchange A[i] and A[k];
      i = k;
    }
    end.
  }