인프런의 영리한 프로그래밍을 위한 알고리즘 강좌를 보고 작성한 문서입니다.

트리(Tree)

계층적인 구조를 표현

• 조직도, 디렉토리와 서브디렉토리 구조, 가계도…

• 트리는 노드(node)들과 노드들을 연결하는 링크(link)들로 구성됨.

부모-자식 관계

• 부모: 위에 있는 노드
• 자식: 아래 있는 노드

형제관계

• 부모가 같은 노드들(루트노드를 제외한 트리의 모든 노드들은 유일한(하나의) 부모 노드를 가진다.)

리프(leaf) 노드

• 자식이 없는 노드들

조상-자손 관계

• 부모-자식의 관계를 확대

부트리(sub tree)

• 트리의 일부를 잘라서 부분만 봐도 하나의 트리이다(전체의 일부분인 트리)

레벨

• 루트에서 밑으로 내려간 정도(0 또는 1부터 시작)

높이

• 서로 다른 레벨의 갯수

트리의 기본적인 성질

• 노드가 N개인 트리는 항상 N-1개의 링크(link)를 가진다.
• 트리에서 루트에서 어떤 노드로 가는 경로는 유일하다. 또한 임의의 두 노드간의 결로도 유일하다.(같은 노드를 두번 이상 방문하지 않는다는 조건하에)

이진 트리(binary tree)

• 이진 트레에서 각 노드는 최대 2개의 자식을 가진다.

• 각각의 자식 노드는 자신이 부모의 왼쪽 자식인지 오른쪽 자식인지가 지정된다.(자식이 한 명인 경우에도)

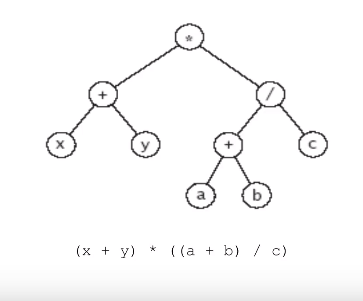
  <이진 트리 응용의 예>
  

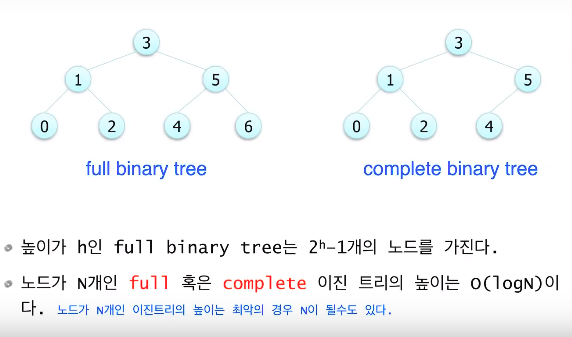
Full and Complete Binary Trees

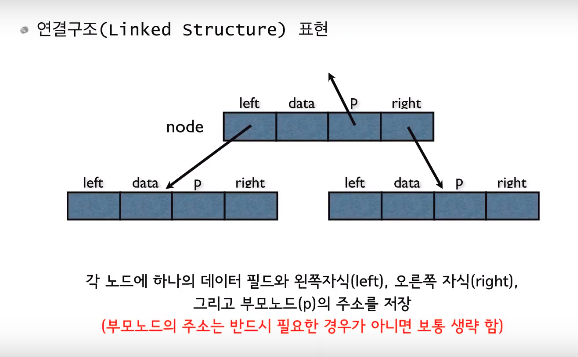
이진트리의 순회(traversal)

• 순회: 이진 트리의 모든 노드를 방문하는 일

• 중순위(inorder) 순회(왼쪽,루트,오른쪽)
• 선순위(preorder) 순회(루트,왼쪽,오른쪽)
• 후순위(postorder) 순회(왼쪽,오른쪽,루트)

• 레벨오더(level-order) 순회

• Inorder-순회

  

  

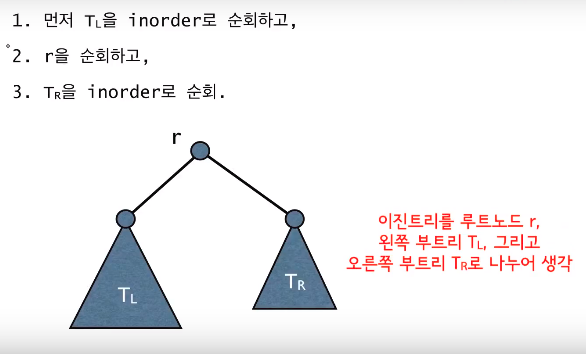
• Preorder & Postorder순회

  

  방문하는 순서만 바뀐다.

• Expression Trees

  

• Level-Order 순회

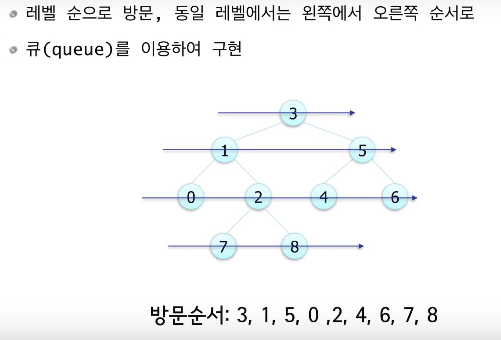
  • 레벨 순으로 방문, 동일 레벨에서는 왼쪽에서 오른쪽 순서로

  • 큐(queue)를 이용하여 구현