인프런의 영리한 프로그래밍을 위한 알고리즘 강좌를 보고 작성한 문서입니다.

최소값 찾기

TREE-MININUM(x)
1   while left[x] != NIL
2     do x <- left[x]
3   return x

최소값은 항상 가장 왼쪽 노드에 존재
시간복잡도: O(h)

최대값 찾기

TREE-MININUM(x)
1   while right[x] != NIL
2     do x <- right[x]
3   return x

최소값은 항상 가장 오른쪽 노드에 존재
시간복잡도: O(h)

Successor

• 노드 x의 successor란 key[x]보다 크면서 가장 작은 키를 가진 노드

• 모든 키들이 서로 다르다고 가정

  

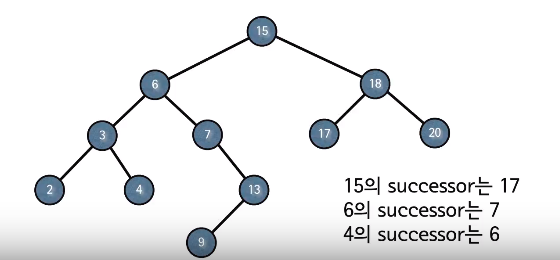
3가지 경우

• 노드 x의 오른쪽 부트리가 존재할 경우, 오른쪽 부트리의 최소값.

• 오른쪽 부트리가 없는 경우, 어떤 노드 y의 왼쪽 부트리의 최대값이 x가 되는 그런 노드 y가 x의 successor

  • 부모를 따라 루트까지 올라가면서 처음으로 누군가의 왼쪽 자식이 되는 노드(위의 그림상에서 13과 15)

• 그런 노드 y가 존재하지 않을 경우 successor가 존재하지 않음(즉, x가 최대값)

수도코드

TREE-SUCCESSOR(x)
1   if right[x] != NIL
2     then return TREE-MINIMUM(right[x])
3   y <- p[x]
4   while y != NIL and x = right[y]
5     do x <- y
6        y <- p[y]
7   return y

시간복잡도: O(h)

Predecessor

• 노드 x의 predecessor란 key[x]보다 작으면서 가장 큰 키를 가진 노드

• Successor와 반대

INSERT

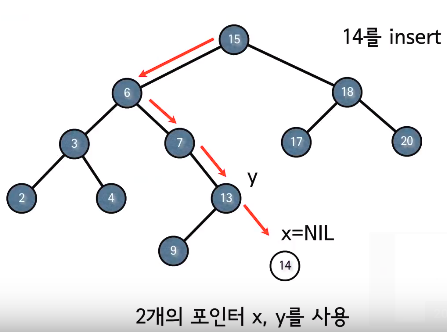
삽입이 일어나는 과정

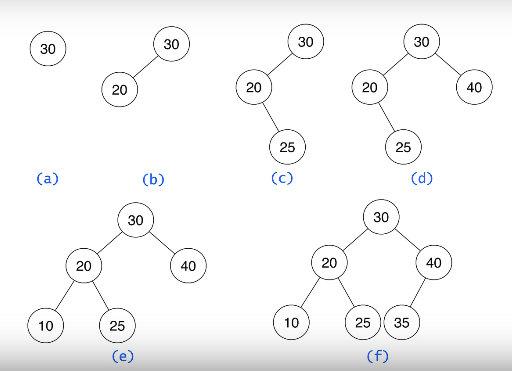
수도코드

시간복잡도: O(h)