인프런의 영리한 프로그래밍을 위한 알고리즘 강좌를 보고 작성한 문서입니다.

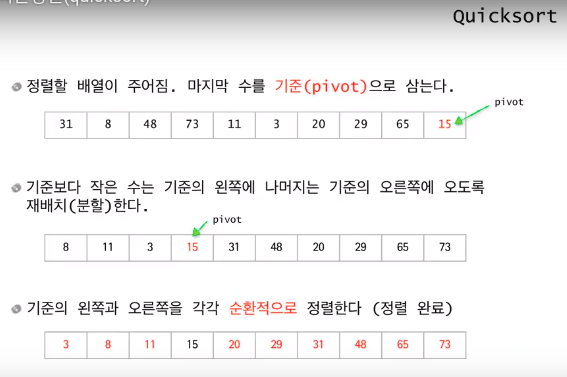
분할정복법

• 분할 배열을 다음과 같은 조건이 만족되도록 두 부분으로 나눈다.

  elements in lower parts <= elements in upper parts

• 정복: 각 부분을 순환적으로 정렬한다.

• 합병: nothing to do

수도코드

quickSort(A[], p, r){
  if(p<r) then {
    q = partition(A, p, r); //분할
    quickSort(A, p, q-1);   //왼쪽 부분배열 정렬
    quickSort(A, q+1, r);   //오른쪽 부분배열 정렬
  }
}

partition(A[], p, r){
  배열 A[p...r]의 원소들을 A[r]을 기준으로 양쪽으로 재배치하고
  A[r]이 자리한 위치를 return 한다;
}

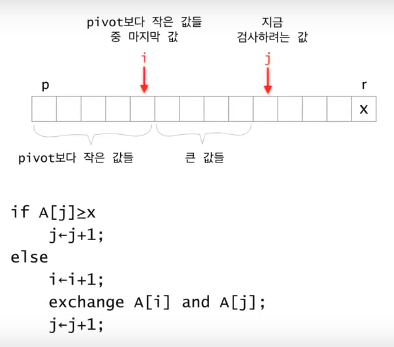
partition 메소드

• x = pivot 값

• pivot의 위치는 고정 하고 i를 기준으로 작은 값, 큰 값을 분류한다.

수도코드

Partition(A, p, r){
  x <- A[r];
  i <- p-1;
  for j<- p to r-1
  if A[j] <= x then
    i <- i+1;
    exchange A[i] and A[j];
  exchange A[i+1] and A[r];
  return i+1;
}

최악의 경우

• 항상 한 쪽은 0개, 다른 쪽은 n-1개로 분할되는 경우

  

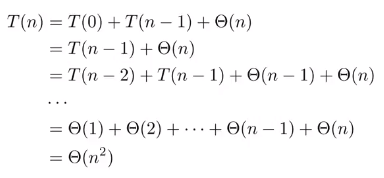
• 이미 정렬된 입력 데이터 (마지막 원소를 피봇으로 선택하는 경우)

최선의 경우

• 항상 절반으로 분할되는 경우

  

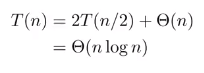
퀵소트가 대체적으로 더 빠른 이유

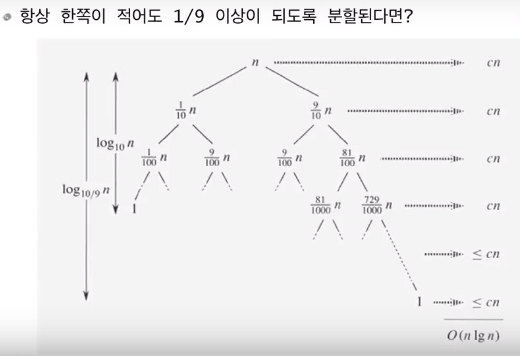
• 일반적으로 최악과 최선의 경우처럼 극단적인 상황은 많지 않다.

• 극단적인 경우만 아니면 “nlogn”의 복잡도로 수렴한다.(위와 같이 1/9만 돼도)

평균시간복잡도

• “평균” 혹은 “기대값”이란?

  

빠른정렬(quicksort) 평균시간복잡도

Pivot의 선택

• 첫번째 값이나 마지막 값을 피봇으로 선택

  • 이미 정렬된 데이터 혹은 거꾸로 정렬된 데이터가 최악의 경우

  • 현실의 데이터는 랜덤하지 않으므로 (거꾸로) 정렬된 데이터가 입력으로 들어올 가능성은 매우 높음

  • 따라서 좋은 방법이라고 할 수 없음

• “Median of Three”

  • 첫번째 값과 마지막 값, 그리고 가운데 값 중에서 중간값(median)을 피봇으로 선택

  • 최악의 경우 시간복잡도가 달리지지는 암ㅎ음

• Randomized Quicksort

  • 피봇을 랜덤하게 선택

  • no worst case instance, but worst case execution (누가 pivot이 될지 정해져있지 않아서 최악의 case가 미리 존재할 수 없다. 하지만 랜덤 선택의 운이 안좋으면 최악의 경우를 실행 시킬 수 있다.)

  • 평균 시간복잡도 O(NlogN)