인프런의 영리한 프로그래밍을 위한 알고리즘 강좌를 보고 작성한 문서입니다.

정렬

비교적 간단하지만 느린 정렬들

• Bubble sort

• Insertion sort

• Selection sort

복잡하지만 조금더 빠른 정렬

• Quicksort

• Merge sort

• Heap sort

근본적으로 다른 정렬

• Radix sort

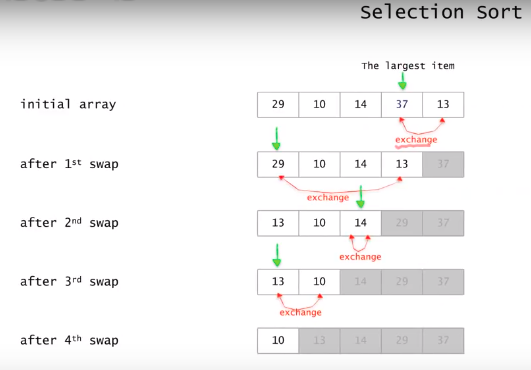
Selection sort(선택 정렬)

• 순서

  1. 가장 큰 값을 찾는다.

  2. 마지막 자리와 자리를 바꾼다.

  3. 다음 큰 값을 찾는다.

  4. 마지막 이전 자리와 자리를 바꾼다.

  5. 마지막 하나가 남을때 까지 반복…

  6. 끝

수도코드

selectionSrot(A[], n){
  //1
  for last <- n downto 2{
    //2
    A[1...last] 중 가장 큰 수 A[k]를 찾는다;
    //3
    A[k] <-> A[last];
  }
}

• 실행시간:

  1. for 루프틑 n-1번 반복

  2. 가장 큰 수를 찾기 위한 비교 횟수: n-1, n-2,…,2,1

  3. 교환은 상수시간 작업

• 시간복잡도

  T(n) = (n-1) + (n-2) + … + 2 + 1 = O(n*n)

최악, 최선, 평균의 복잡도가 동일

Bubble sort(버블정렬)

기본 아이디어는 선택정렬이랑 유사하다.

• 순서

  1. 첫번째와 두번째 값과 비교한다.

  2. 첫번째 값이 더 크면 자리를 바꾼다.

  3. 두번째 값과 세번째 값을 비교한다.

  4. 두번째 값이 더 크면 자리를 바꾼다.

  5. 반복

  6. n-1번째 값과 n번째 자리를 비교한다.

  7. n-1번째 값이 더 크면 자리를 바꾼다.

  8. n번째를 빼고, n-1번째 까지 1~7번 작업을 반복한다.

수도코드

bubbleSort(A[], n){
  //1
  for last <- n downto 2{
    //2
    for i <- 1 to last-1{
      //3
      if(A[i] > A[i+1]) then A[i] <-> A[i+1];
    }
  }
}

• 수행시간:

  1. for 루프는 n-1번 반복

  2. for 루프는 각각 n-1, n-2,…,2,1번 반복

  3. 교환은 상수시간 작업

• 시간복잡도

  T(n) = (n-1) + (n-2) + … + 2 + 1 = O(n*n)

최악, 최선, 평균의 복잡도가 동일

Insertion Sort(삽입정렬)

• 순서

  1. 두번째와 첫번째를 비교하여 정렬한다.

  2. 세번째와 앞의 정렬이 된 배열과 비교하여 정렬한다.

  3. 네번째와 앞의 정렬이 된 배열과 비교하여 정렬한다.

  4. n번째와 앞의 정렬이 된 배열과 비교하여 정렬한다.

• n번째의 데이터를 배열과 비교할때 앞에서부터 비교하는 것보단 뒤에서부터 비교하는게 더 효율 적이다.

  • 앞에서부터 비교하면 아래와 같이 작업 한다.

    1. 앞에서부터 비교

    2. 뒤의 데이터들을 이동

  • 뒤에서부터 비교하면 아래와 같다.

    1. 뒤에서부터 비교하며 더 큰 값은 뒤로 이동시키며 자신의 자리를 찾는다.

  • 차이점은 앞에 있는 데이터들을 비교하지 않아도 되서 더 효율적이다.

수도코드

insertionSort(A[], n){
  //1
  for i <- 2 to n{
    //2
    A[1...i]의 적당한 자리에 A[i]를 삽입한다.
  }

}

• 수행시간:
  1. for 루프는 n-1번 반복
  2. 삽입은 최악의 경우 i-1번 비교
• 최악의 경우:
  T(n) = (n-1) + (n-2) + … + 2 + 1 = O(n*n)

최악의 경우는 선택,버블 정렬이랑 동일하지만 최선의 경우는 n-1 이다.