인프런의 영리한 프로그래밍을 위한 알고리즘 강좌를 보고 작성한 문서입니다.

Prim의 알고리즘

• 임의의 노드를 출발노드로 선택

• 출발 노드를 포함하는 트리를 점점 키워 감.

• 매 단계에서 이미 트리에 포함된 노드와 포함되지 않은 노드를 연결하는 에지들 중 가장 가중치가 작은 에지를 선택

  

예)

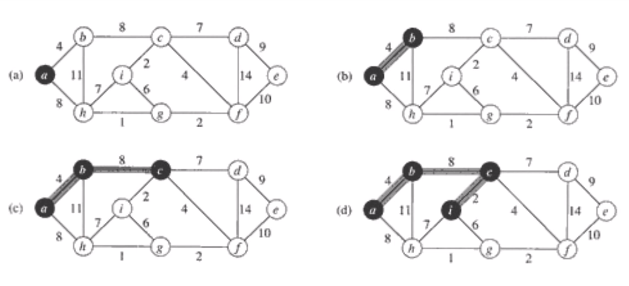
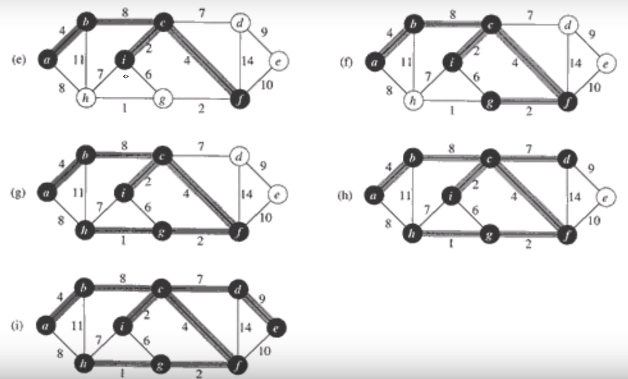
왜 MST가 찾아지는가?

• prim의 알고리즘의 임의의 한 단계를 생각해보자.

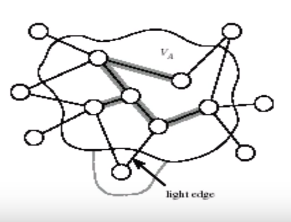
• A를 현재까지 알고리즘이 선택한 에지의 집합이라고 하고, A를 포함하는 MST가 존재한다고 가정하자.

  

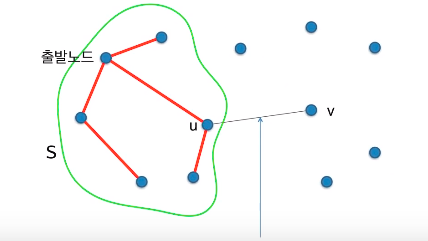
  출발 노드에 이미 연결된 노드와 그렇지 않은 노드를 연결하는 에지들 중 lightest edge

가중치가 최소인 에지 찾기

가중치가 최소인 에지 찾기

• 가중치가 최소인 에지를 찾는 대신 key값이 최소인 노드를 찾는다.

  

  

  

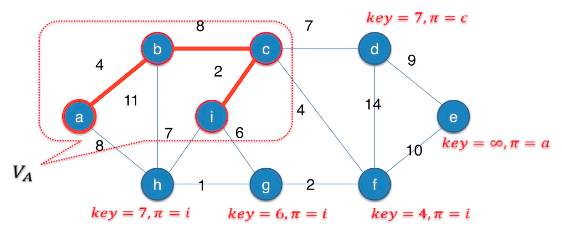
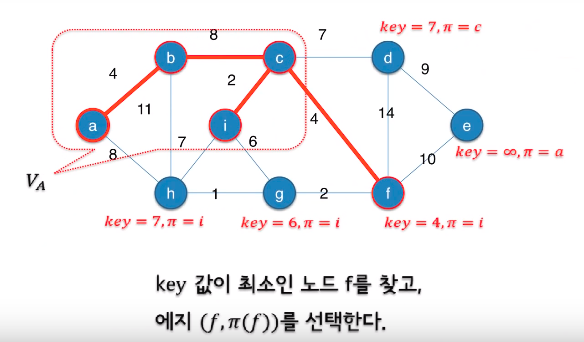
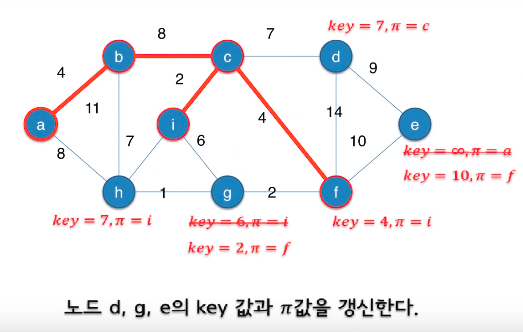
Prim의 알고리즘

Key값이 최소인 노드 찾기

• 최소 우선순위 큐를 사용

  • V - VA에 속한 노드들을 저장

  • Extract-Min : Key값이 최소인 노드를 삭제하고 반환

  

Prim의 알고리즘 : 시간복잡도

• 이진 힙(binary heap)을 사용하여 우선순위 큐를 구현한 경우

• while loop :

  • n번의 Extract-Min 연산 : O(nlongn)

  • m번의 Decrease-Key 연산 : O(mlongn)

• 따라서 시간복잡도 : O(nlong + mlogn) = O(mlogn)

• 우선순위 큐를 사용하지 않고 단순하게 구현할 경우 : O(n^2)

• Fibonacci 힙을 사용하여 O(m+nlogn)에 구현 가능 [Fredman-Tarjan 1984]