인프런의 영리한 프로그래밍을 위한 알고리즘 강좌를 보고 작성한 문서입니다.

최소신장트리(Minimum Spanning Tree)

• 입력 : n개의 도시, 도시와 도시를 연결하는 비용

• 문제 : 최소의 비용으로 모든 도시들이 서로 연결되게 한다.

  

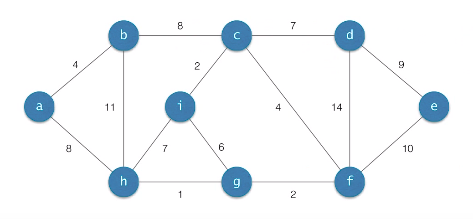
  해가 유일하지는 않음

• 무방향 가중치 그래프 G = ( V, E )

• 각 에지 (u, V ) ∈ E 에 대해서 가중치 w( u, V )

  

왜 트리라고 부르나?

• 싸이클이 없는 연결된(connected) 무방향 그래프를 트리라고 부른다.

• MST 문제의 답은 항상 트리가 된다. 왜?

  

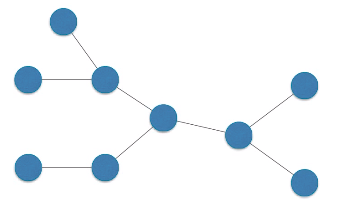
  노드가 n개인 트리는 항상 n-1개의 에지를 가짐

Generic MST 알고리즘

• 어떤 MST의 부분집합 A에 대해서 AU{(u,V)}도 역시 어떤 MST의 부분 집합이 될 경우 에지 (u, V)는 A에 대해서 안전하다(safe)고 한다.

• Generic MST 알고리즘:

  1. 처음에는 A=∅ 이다.
  2. 집합 A에 대해서 안전한 에지를 하나 찾은 후 이것을 A에 더한다.
  3. 에지의 개수가 n-1개가 될 때까지 2번을 반복한다.

안전한 에지 찾기

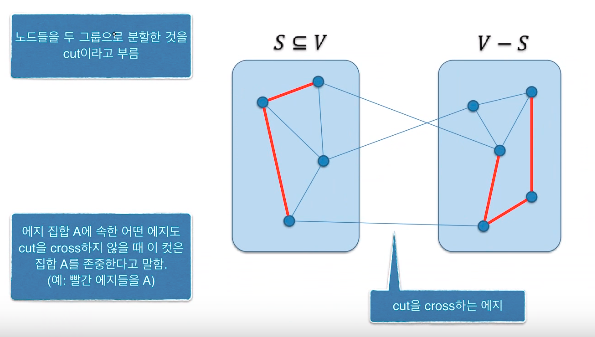
• 그래프의 정점들을 두 개의 집합 S와 V-S로 분할한 것을 컷(cut) (S, V-S)라고 부른다.

• 에지 (u, V)에 대해서 u ∈ V-S일 때 에지 (u, V)는 컷 (S, V-S)를 cross한다고 말한다.

• 에지들의 부분집합 A에 속한 어떤 에지고 컷 (S, V-S)를 cross하지 않을 때 컷 (S, V-S)는 A를 존중한다(respect)고 말한다.

  

• A가 어떤 MST의 부분집합이고, (S, V-S)는 A를 존중하는 컷이라고 하자. 이 컷을 cross하는 에지들 중 가장 가중치가 작은 에지 (u, V)는 A에 대해서 안전하다.